
| A. | $\frac{25}{4}$ | B. | $\frac{15}{2}$ | C. | 4 | D. | 6 |
分析 求出椭圆的a,b,c,e,分别运用椭圆的第二定义,求得点到左焦点的距离,再由第一定义,即可得到所求距离.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的a=5,b=3,c=$\sqrt{{a}^{2}-{b}^{2}}$=4,
e=$\frac{c}{a}$=$\frac{4}{5}$,
设点到左焦点的距离为d,点到右焦点的距离为k,
利用椭圆的第二定义:$\frac{d}{5}$=e=$\frac{4}{5}$,
解得d=4,
再由椭圆的第一定义:d+k=10,
解得:k=6,
故选D.
点评 本题考查的知识要点:椭圆的离心率的应用,椭圆的第一、第二定义的应用.定义法解题是处理圆锥曲线问题中常用方法,要掌握.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | |x1-(a+bx1)|+|x2-(a+bx2)|+|x3-(a+bx3)| | B. | [x1-(a+bx1)]2+[x2-(a+bx2)]2+[x3-(a+bx3)]2 | ||
| C. | |y1-(a+bx1)|+|y2-(a+bx2)|+|y3-(a+bx3)| | D. | [y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=0 | B. | x=2 | C. | y=2 | D. | y=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
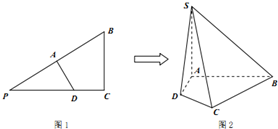 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
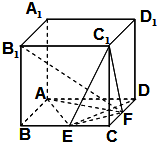 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com