
【题目】已知椭圆E的右焦点与抛物线![]() 的焦点重合,点M
的焦点重合,点M![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设![]() ,直线
,直线![]() 与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求
与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2x+![]() (x∈R).
(x∈R).
(1)当x∈(0,1]时,求f(x)的解析式.
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,![]() 是下底面圆
是下底面圆![]() 的直径,
的直径,![]() 是上底面圆
是上底面圆![]() 的直径,
的直径,![]() 是圆台的一条母线.
是圆台的一条母线.
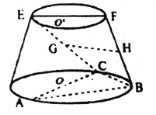
(Ⅰ)已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如下图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
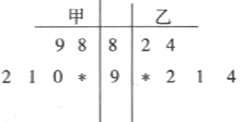
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶段序”,当且仅当两个
阶段序”,当且仅当两个![]() 阶色序对应位置上的颜色至少有一个不相同时,称为不同的
阶色序对应位置上的颜色至少有一个不相同时,称为不同的![]() 阶色序.若某圆的任意两个“
阶色序.若某圆的任意两个“![]() 阶段序”均不相同,则称该圆为“
阶段序”均不相同,则称该圆为“![]() 阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
A.4 B.6
C. 8 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com