练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知P是椭圆$\frac{x^2}{100}+\frac{y^2}{36}=1$上的一点，若P到椭圆右准线的距离是$\frac{17}{2}$，则点P到左焦点的距离是$\frac{66}{5}$．

    分析 利用椭圆的第二定义，可求P到右焦点的距离，然后再根据椭圆的第一定义求出它到左焦点的距离．

    解答 解：设F1、F2分别为椭圆的左、右焦点，
    P到右准线的距离为d2=$\frac{17}{2}$，
    由椭圆的第二定义知，$\frac{|P{F}_{2}|}{{d}_{2}}$=$\frac{c}{a}$=$\frac{8}{10}$，解得|PF2|=$\frac{34}{5}$，
    又|PF1|+|PF2|=2a=20，解得|PF1|=$\frac{66}{5}$
    故P到它的左焦点的距离为$\frac{66}{5}$．
    故答案：$\frac{66}{5}$．

    点评 本题主要考查椭圆的基本性质，椭圆的定义的应用，考查计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．公差为正数的等差数列{an}中，a2+a5=12，a3a4=35，则数列{$（\frac{1}{2}）^{{a}_{n}}$}的前n项和为（　　）
    A．Sn=1-$\frac{1}{{2}^{n}}$B．Sn=$\frac{2}{3}$-$\frac{2}{3•{4}^{n}}$C．Sn=2n+1-2D．Sn=$\frac{{4}^{n+1}-4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，椭圆上异于M、N于点P满足kPM•kPN=-$\frac{1}{4}$，则椭圆的离心率为（　　）
    A．$\frac{{\sqrt{2}}}{2}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点A（1，$\frac{\sqrt{2}}{2}$），且离心率为$\frac{\sqrt{2}}{2}$．
    （1）求椭圆的标准方程；
    （2）过右焦点的直线l与椭圆C相交于P，Q两点，F1为左焦点，且$\overrightarrow{{F}_{1}P}$⊥$\overrightarrow{{F}_{1}Q}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

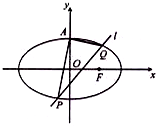    13．已知椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的上顶点为A，直线l：y=kx+m交椭圆P，Q两点，设直线AP，AQ的斜率分别为k1，k2．
    （1）若m=0，时求k1•k2的值；
    （2）若k1•k2=-1时，证明直线l：y=kx+m过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在棱锥A-BCDE中，∠BAC=$\frac{π}{2}$，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．
    （1）求证：EF⊥AD；
    （2）求三棱锥F-ADE的高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

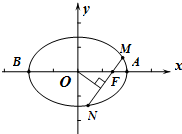    10．如图：已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆，A，B为顶点，过右焦点的弦MN的长度为y，中心O到弦MN的距离为d，点M从右顶点A开始按逆时针方向在椭圆上移动到B停止，当0°≤∠MFA≤90°时，记x=d，当90°＜∠MFA≤180°，记x=2$\sqrt{2}$-d，函数y=f（x）图象是（　　）
    A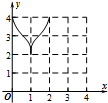．B．C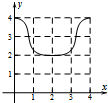．D．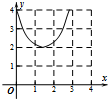

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与双曲线x2-$\frac{{y}^{2}}{2}$=1有公共的焦点，且它们的离心率互为倒数，则该椭圆的方程是$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{6}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）=$\frac{{x}^{2}（x+1）}{x+1}$是（　　）
    A．奇函数B．偶函数
    C．既是奇函数又是偶函数D．非奇非偶函数

    查看答案和解析>>

    同步练习册答案