
分析 (1)p:m-1>5-m>0,解出m范围,由于?p为真命题,可得p为假命题,即可得出.
(2)函数有零点,可得△≥0,由于“p∨q”为真,可得m∈P∪Q.
解答 解:(1)p:m-1>5-m>0,∴3<m<5,…(3分)
∵?p为真命题,∴p为假命题…(4分)
∴m≤3或m≥5.…(5分)
(2)函数有零点,∴△≥0,$(2m)^{2}-4×3(m+\frac{4}{3})$≥0,…(6分)
∴m≥4或m≤-1.…(8分)
设Q={m|m≥4或m≤-1},P={m|3<m<5}.
∵“p∨q”为真,∴m∈P∪Q,即m>3或m≤-1.…(10分)
点评 本题考查了不等式的性质、集合的运算性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
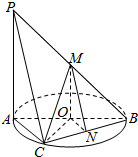 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
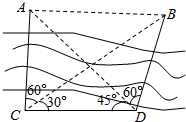 如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.
如图,A、B两点都在河的对岸(不可到达),测量者在河岸边选定两点C、D,测得CD=40m,并且在C、D两点分别测得∠ACB=60°,∠ADB=60°∠BCD=30°,∠ADC=45°,求河的对岸的两点A、B间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com