
分析 (1)利用有理指数幂求解即可.
(2)(3)利用对数的运算法则求解即可.
解答 解:(1)$\frac{1-{a}^{-\frac{1}{2}}}{1+{a}^{-\frac{1}{2}}}$-$\frac{2{a}^{\frac{1}{2}}}{a-1}$=$\frac{(1-{a}^{-\frac{1}{2}})^{2}}{(1+{a}^{-\frac{1}{2}})(1-{a}^{-\frac{1}{2}})}$-$\frac{2{a}^{\frac{1}{2}}}{a-1}$=$\frac{1-2{a}^{-\frac{1}{2}}+{a}^{-1}}{1-{a}^{-1}}+\frac{2{a}^{\frac{1}{2}}}{1-a}$=$\frac{1-2{a}^{\frac{1}{2}}+a}{a-1}-\frac{2{a}^{\frac{1}{2}}}{a-1}$$\frac{1+a}{a-1}$=
(2)2${\;}^{3+lo{g}_{2}5}$=8•${2}^{{log}_{2}5}$=40.
(3)lg5•lg20+(lg2)2=2lg5•lg2+(lg5)2+(lg2)2=(lg2+lg5)2=1
点评 本题考查对数的运算法则的应用,有理指数幂的化简求值,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
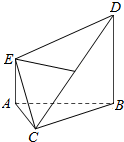 在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.
在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②④ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com