练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．若m＜0，则不等式35x2-2mx＜m2的解集为（$\frac{m}{5}$，-$\frac{m}{7}$）．

    分析 原不等式化为（5x-m）（7x+m）＜0，则（5x-m）（7x+m）=0的两个根为x1=$\frac{m}{5}$＜0，x2=-$\frac{m}{7}$＞0，继而得到不等式的解集．

    解答 解：35x2-2mx＜m2化为35x2-2mx-m2＜0，
    即为（5x-m）（7x+m）＜0，
    ∵（5x-m）（7x+m）=0的两个根为x1=$\frac{m}{5}$＜0，x2=-$\frac{m}{7}$＞0，
    ∴不等式35x2-2mx＜m2的解集为（$\frac{m}{5}$，-$\frac{m}{7}$），
    故答案为：（$\frac{m}{5}$，-$\frac{m}{7}$）．

    点评 本题考查了一元二次不等式的解法，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届江西南昌新课标高三一轮复习训练三数学试卷（解析版） 题型：解答题

    已知函数（为常数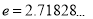，是自然对数的底数），曲线在点处的切线与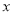轴平行．

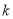    （1）求的值；

    （2）求的单调区间；

    （3）设，其中为的导函数．证明：对任意，．

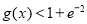    查看答案和解析>>

    科目：高中数学 来源：2017届安徽淮北十二中高三上月考二数学（文）试卷（解析版） 题型：选择题

    集合，则（ ）

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知圆C：x2+y2=r2具有如下性质：若M，N是圆C上关于原点对称的两个点，点P是圆C上任意一点，当直线PM，PN的斜率都存在时，记为kPM，kPN，则kPM与kPN之积是一个与点P的位置无关的定值．利用类比思想，试对椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$写出具有类似特征的性质，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．将英文单词“believe”的7个字母重新排列，要求恰有2个“e”相邻，则不同的排列方法有480种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知点H为△ABC的垂心，且$\overrightarrow{HA}$$•\overrightarrow{HB}$=-3，则$\overrightarrow{BH}$$•\overrightarrow{HC}$的值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．如图：已知矩形BB1C1C所在平面与底面ABB1N垂直，直角梯形ABB1N中AN∥BB1，AB⊥AN，CB=BA=AN=2，BB1=4．
    （Ⅰ）求证：BN⊥平面C1B1N；（Ⅱ）求二面角C-C1N-B1的正弦值；
    （Ⅲ）在BC边上找一点P，使B1P与CN所成角的余弦值为$\frac{{5\sqrt{51}}}{51}$，并求线段B1P的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．函数y=$\sqrt{x（10-3x）}$（0＜x＜$\frac{10}{3}$）的最大值为$\frac{5\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=ax2-blnx在点（1，f（1））处的切线为y=1．
    （Ⅰ）求实数a，b的值；
    （Ⅱ）当x∈（0，1）时，求证：f（x）＞x2-x+1
    （Ⅲ）若0＜x1＜x2，求证：$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$＜2x2．

    查看答案和解析>>

    同步练习册答案