Question

16．如图：已知矩形BB₁C₁C所在平面与底面ABB₁N垂直，直角梯形ABB₁N中AN∥BB₁，AB⊥AN，CB=BA=AN=2，BB₁=4．
（Ⅰ）求证：BN⊥平面C₁B₁N；（Ⅱ）求二面角C-C₁N-B₁的正弦值；
（Ⅲ）在BC边上找一点P，使B₁P与CN所成角的余弦值为$\frac{{5\sqrt{51}}}{51}$，并求线段B₁P的长．

Answer 1

分析 （Ⅰ）证明AB⊥BB₁，建立空间直角坐标系，证明B₁N⊥BN，BN⊥B₁C₁，然后证明BN⊥平面C₁B₁N．
（Ⅱ）求出平面法C₁B₁N向量$\overrightarrow{m}=（x，y，z）$，设二面角二面角C-C₁N-B₁的平面角为θ，求出平面C₁CN的法利用向量的数量积求解即可．
（Ⅲ）设P（0，0，a）为BC上一点，推出$\overrightarrow{{B_1}P}=（0，-4，a）$，通过$\frac{5\sqrt{51}}{51}$=$\frac{|\overrightarrow{{B}_{1}P}•\overrightarrow{CN}|}{\left|\overrightarrow{{B}_{1}P}\right|\left|\overrightarrow{CN}\right|}$，求解P，然后求解线段B₁P的长度．

解答 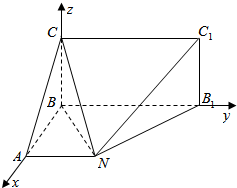（Ⅰ）证明：∵矩形BB₁C₁C所在平面与底面ABB₁N垂直，则CB⊥底面ABB₁N，
∵AN∥BB₁，AB⊥AN，则AB⊥BB₁，建立如图所示的空间直角坐标系，则知
N（2，2，0），C₁（0，4，2），B₁（0，4，0），C（0，0，2），
∵$\overrightarrow{{B_1}N}•\overrightarrow{BN}=4-4=0$，则B₁N⊥BN，BN⊥B₁C₁，
且B₁N∩B₁C₁=B₁，则BN⊥平面C₁B₁N．
（Ⅱ）解：设平面法C₁B₁N向量为$\overrightarrow{m}=（x，y，z）$
∵$\overrightarrow{BN}$=（2，2，0），∴设$\overrightarrow{BN}$=$2\overrightarrow{m}$，则求得$\overrightarrow{m}$=（1，1，0）．
设二面角二面角C-C₁N-B₁的平面角为θ，
设平面C1CN的法向量为：$\overrightarrow{n}$=（x，y，z），
则$\overrightarrow{n}•\stackrel{\;}{\overrightarrow{{CC}_{1}}=0}$，$\overrightarrow{n}•\stackrel{\;}{\overrightarrow{{CN}_{\;}}=0}$，由$\left\{{\begin{array}{l}{y=0}\\{x-z=0}\end{array}}\right.$．
得$\overrightarrow{n}$=（1，0，1）
cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$=$\frac{1}{2}$，∴$sinθ=\frac{\sqrt{3}}{2}$．
（Ⅲ）解：设P（0，0，a）为BC上一点，则$\overrightarrow{{B_1}P}=（0，-4，a）$，$\overrightarrow{CN}$=（2，2，-2），
则有$\frac{5\sqrt{51}}{51}$=$\frac{|\overrightarrow{{B}_{1}P}•\overrightarrow{CN}|}{\left|\overrightarrow{{B}_{1}P}\right|\left|\overrightarrow{CN}\right|}$，则a²-17a+16=0，解得a=1．
∴P（0，0，1），$\overrightarrow{{B}_{1}P}=（0，-4，1）$，
∴$\overrightarrow{{|B}_{1}P}|=\sqrt{{0}^{2}+（-4）^{2}+{1}^{2}}$=$\sqrt{17}$
则线段B₁P的长度为$\sqrt{17}$．

点评 本题考查空间向量的应用，二面角的平面角的求法，空间距离公式的应用，直线与平面垂直的判定定理的应用，考查计算能力以及逻辑推理能力．