
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为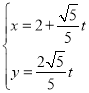 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 交
交![]() 于
于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方),
轴上方),![]() 交极轴于点
交极轴于点![]() (异于极点
(异于极点![]() ).
).
(1)求![]() 的直角坐标方程和
的直角坐标方程和![]() 的直角坐标;
的直角坐标;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上的点,求
上的点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;直角坐标为
;直角坐标为![]() .(2)
.(2)![]()
【解析】
(1)把![]() 两边同时乘以
两边同时乘以![]() ,结合
,结合![]() ,可得
,可得![]() 的直角坐标方程,取
的直角坐标方程,取![]() ,可得点
,可得点![]() 的直角坐标.
的直角坐标.
(2)设![]() 所对应的参数分别为t1,t2(t1>0),将
所对应的参数分别为t1,t2(t1>0),将 代入
代入![]() ,得到关于
,得到关于![]() 的一元二次方程,求得
的一元二次方程,求得![]() ,进一步得到
,进一步得到![]() 的坐标,再求出
的坐标,再求出![]() 的圆心
的圆心![]() ,可得
,可得![]() ,则
,则![]() 的最小值可求.
的最小值可求.
解法一:(1)由![]() 及
及![]() ,得
,得![]() ,即
,即![]() ,
,
所以圆![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
令![]() ,得
,得![]() 或0(舍去),所以点
或0(舍去),所以点![]() 的直角坐标为
的直角坐标为![]() .
.
(2)设![]() ,
,![]() 所对应的参数分别为
所对应的参数分别为![]() ,
,![]() (其中
(其中![]() ),
),
将 代入
代入![]() 得,
得,![]() ,
,
解得![]() 或
或![]() ,所以
,所以![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
依题意,![]() 的圆心
的圆心![]() ,所以
,所以![]() ,
,
所以![]() 最小值为
最小值为![]() .
.
解法二:(1)同解法一;
(2)将直![]() 的参数方程
的参数方程 (
(![]() 为参数),消去
为参数),消去![]() 得
得![]() ,
,
即![]() 的普通方程为
的普通方程为![]() ,由
,由![]() 得
得![]() ,
,
解得![]() 或4,所以
或4,所以![]() ,又
,又![]() ,
,
因为![]() 为
为![]() 中点,即
中点,即![]() ,
,
依题意,![]() 的圆心
的圆心![]() ,所以
,所以![]() ,
,
所以![]() 最小值为
最小值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

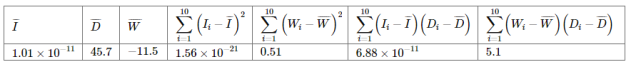
表中![]() ,
,![]()
(1)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程
的回归方程![]() ;
;
(2)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪声污染的干扰,并说明理由.
点是否受到噪声污染的干扰,并说明理由.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: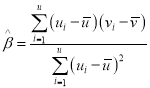 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占50%,苹果销量约占20%,三星销量约占30%).根据该图,以下结论中一定正确的是( )
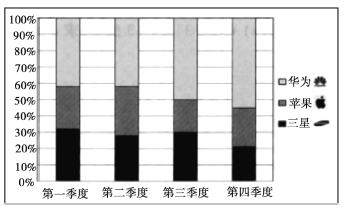
A.华为的全年销量最大B.苹果第二季度的销量大于第三季度的销量
C.华为销量最大的是第四季度D.三星销量最小的是第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:

设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn.
(1)求p2的值;
(2)证明:pn>![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的两截面面积都相等,则两几何体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足祖暅原理,则该不规则几何体的体积为( )
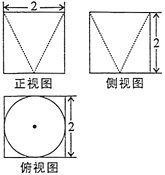
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com