考点:三角函数线
专题:三角函数的图像与性质
分析:根据三角函数线的定义(1)过点(0,-
)作x轴的平行线交单位圆于P和P',在[0,2π)内找出当当-
<x<
时,sinα>-
成立,再由终边相同的角的集合,即可得到所有满足条件的角的集合.
(2)找出余弦值等于
的角度对应的三角函数线,再利用终边相同角的余弦求满足条件的α值.
(3)过点(1,1)和原点作直线交单位圆于P和P′,找到对应的正切值为1的三角函数线,再根据终边相同角找出所有满足条件的角.
解答:
解:(1)如图所示,过点(0,-
)作x轴的平行线,交单位圆于P和P',
则sin∠POx=sin∠P'Ox=-
∵在[0,2π)内,满足条件sinα=-
的∠P'Ox=
,∠POx=
观察图形可得:当-
<x<
时,sinα>-
成立,
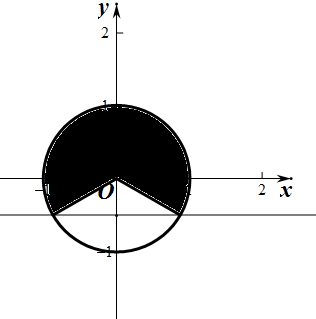
∴满足条件sinα>-
的角α的集合是{x|
-+2kπ<x<
+2kπ,k∈Z};
(2)∵在[0,2π)内,cos
=cos
=
,由余弦线可知,
满足cosα>
的终边在如图的弧内,
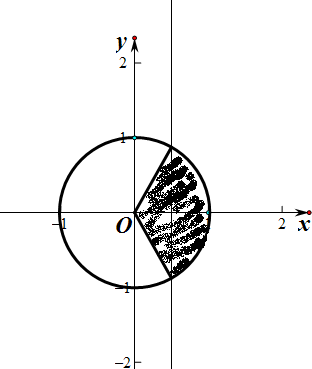
∴cosα>
的解集为{α|-
+2kπ<α<2kπ+
};
(3)过点(1,1)和原点作直线交单位圆于P和P′,
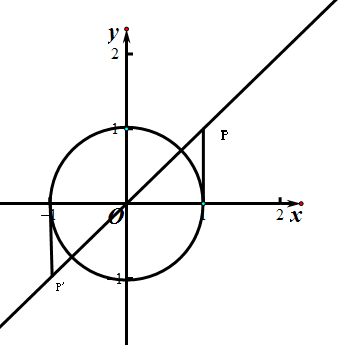
则射线OP、OP′就是满足tanα=1的角α的终边
∵在[0,2π)内,满足条件的∠POx=π-
=,
∠P′Ox=
∴满足条件tanα>1的角α的集合是{x|
+kπ<x<
+kπ或
+π<x<
+kπ,k∈Z}.
点评:本题给出满足条件的角,要求利用单位圆找出角α的集合.着重考查了单位圆中的三角函数线、终边相同角的集合等知识,属于基础题.






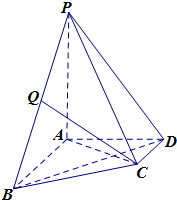 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2