
分析 (1)由题意可知:Sn+1=2an+1-2(n+1),Sn=2an-2n,两式相减得:an+1=2an+1-2an-2,整理得:an+1+2=2(an+2),由bn=an+2,可知:$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}+2}{{a}_{n}+2}$=2,可知数列{bn}是等比数列,根据等比数列通项公式求得${b_n}=4•{2^{n-1}}={2^{n+1}}$,代入即可求得${a_n}={2^{n+1}}-2$;
(2)由(1)求出nan,根据分组求和法、错位相减法,等比、等差数列的前n项和公式求出Tn.
解答 解:(1)证明:∵Sn=2an-2n对于任意的正整数都成立,
∴Sn+1=2an+1-2(n+1),
两式相减,得Sn+1-Sn=2an+1-2(n+1)-2an+2n,
∴an+1=2an+1-2an-2,即an+1=2an+2,
∴an+1+2=2(an+2),
∴$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}+2}{{a}_{n}+2}$=2,对一切正整数都成立.
∴数列{bn}是等比数列.
由已知得 S1=2a1-2即a1=2a1-2,
∴a1=2,
∴首项b1=a1+2=4,公比q=2,
∴${b_n}=4•{2^{n-1}}={2^{n+1}}$.
∴${a_n}={2^{n+1}}-2$;
(2)∵nan=n•2n+1-2n,
∴{nan}的前n项和Tn,
Tn=1•22+2•23+…+n•2n+1-2(1+2+…+n)
=1•22+2•23+…+n•2n+1-2×$\frac{n(n+1)}{2}$,
=1•22+2•23+…+n•2n+1-n(n+1)
令cn=n•2n+1,数列{cn}前n项和Cn,
Cn=1•22+2•23+…+n•2n+1,①
2Cn=1•23+2•24+…+n•2n+2,②
由①-②得:-Cn=22+23+…+2n+1-n•2n+2
=$\frac{4(1-{2}^{n})}{1-2}$-n•2n+2,
=2n+2-4-n•2n+2
=(1-n)2n+2-4,
∴Cn=(n-1)2n+2+4
∴Tn=(n-1)2n+2+4-n(n+1).
点评 本题考查等比数列的定义、通项公式、前n项和公式,Sn与an的关系式,以及分组求和法、错位相减法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [$\frac{1}{2}$,1] | C. | [-$\frac{1}{2}$,1] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
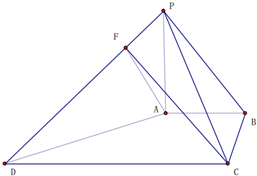 如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,
如图,在四棱锥P-ABCD中,已知AB=1,BC=2,CD=4,AB∥CD,BC⊥CD,平面PAB⊥平面ABCD,PA⊥AB,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | (-1,1) | C. | ∅ | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com