
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
分析 直线l:y=kx-1与曲线f(x)=x-1+$\frac{1}{{e}^{x}}$没有公共点,则x-1+$\frac{1}{{e}^{x}}$=kx-1无解,可化为k=1+$\frac{1}{x{e}^{x}}$,设g(x)=1+$\frac{1}{x{e}^{x}}$,求导,研究此函数的单调性即可解决
解答 解:若直线l:y=kx-1与曲线f(x)=x-1+$\frac{1}{{e}^{x}}$没有公共点,则x-1+$\frac{1}{{e}^{x}}$=kx-1无解,
∵x=0时,上述方程不成立,∴x≠0
则x-1+$\frac{1}{{e}^{x}}$=kx-1可化为k=1+$\frac{1}{x{e}^{x}}$,
设g(x)=1+$\frac{1}{x{e}^{x}}$,
∴g′(x)=$\frac{-(x+1)}{{x}^{2}{e}^{x}}$
∴g′(x)满足:在(-∞,-1)上g′(x)>0,在(-1,0)上g′(x)<0,在(0,+∞)上g′(x)<0,
∴g(x)满足:在(-∞,-1)上递增,在(-1,0)上递减,在(0,+∞)上递减,
g(-1)=1-e,而当x→+∞时,g(x)→1,
∴g(x)的图象: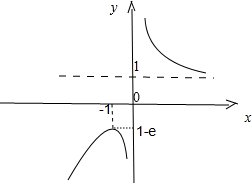
∴g(x)∈(-∞,1-e]∪(1,+∞)
无解时,k∈(1-e,1],
∴kmax=1,
故选:C
点评 本题考查导数的应用,考查函数的最值的求法,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 对称中心为$(\frac{π}{3},0)$ | |
| B. | 函数y=sin2x向左平移$\frac{5π}{6}$个单位可得到f(x) | |
| C. | f(x)在区间$(-\frac{2π}{3},-\frac{π}{6})$上递增 | |
| D. | 方程f(x)=0在区间$[-\frac{5π}{6},0]$上有三个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③④ | C. | ③④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3)∪(2,+∞) | B. | (-6,1) | C. | (-∞,-6)∪(1,+∞) | D. | (-3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com