
分析 (Ⅰ)由条件利用同角三角函数的基本关系,求得cosα,tanβ的值.
(Ⅱ)由条件利用两角和的正切公式,求得要求式子的值.
解答 解:(Ⅰ)∵sinα=$\frac{\sqrt{5}}{5}$,cosβ=$\frac{3\sqrt{10}}{10}$,α∈($\frac{π}{2}$,π),β∈(-$\frac{π}{2}$,0),
∴cosα=-$\sqrt{1-sin2α}$=-$\frac{2\sqrt{5}}{5}$.
sinβ=-$\sqrt{1-cos2β}$=-$\frac{\sqrt{10}}{10}$,进而tanβ=$\frac{sinβ}{cosβ}$=-$\frac{1}{3}$.
(Ⅱ)由(Ⅰ)知,tanα=$\frac{sinα}{cosα}$=-$\frac{1}{2}$,tanβ=-$\frac{1}{3}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{-\frac{1}{2}-\frac{1}{3}}{1-(-\frac{1}{2})•(-\frac{1}{3})}$=-1.
点评 本题主要考查同角三角函数的基本关系,两角和的正切公式的应用,属于基础题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:填空题
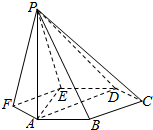 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
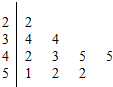 近日有媒体在全国范围开展“2015年国人年度感受”的调查,在某城市广场有记者随机访问10个步行的路人,其年龄的茎叶图如下:
近日有媒体在全国范围开展“2015年国人年度感受”的调查,在某城市广场有记者随机访问10个步行的路人,其年龄的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
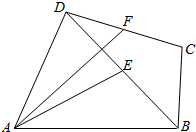 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10% | B. | 15% | C. | 16% | D. | 20% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com