
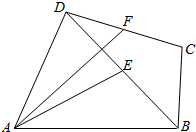
 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.分析 (1)由已知结合共线向量基本定理得答案;
(2)由已知结合向量加法、减法的运算法则求解;
(3)由向量加法、减法及向量的数量积运算得答案.
解答 解:(1)∵E,F分别为BD,DC的中点,
∴$\overrightarrow{EF}=\frac{1}{2}\overrightarrow{BC}$,则$\overrightarrow{AF}=\overrightarrow{AE}+\overrightarrow{EF}=\overrightarrow{AE}+\frac{1}{2}\overrightarrow{BC}$;
(2)${\overrightarrow{AB}}^{2}+{\overrightarrow{AD}}^{2}=(\overrightarrow{AE}+\overrightarrow{EB})^{2}+(\overrightarrow{AE}+\overrightarrow{ED})^{2}$
=$(\overrightarrow{AE}+\overrightarrow{EB})^{2}+(\overrightarrow{AE}-\overrightarrow{EB})^{2}=2{\overrightarrow{AE}}^{2}+2{\overrightarrow{EB}}^{2}=2×{3}^{2}+2×{2}^{2}=26$;
(3)$\overrightarrow{AC}•\overrightarrow{AD}=(\overrightarrow{AF}+\overrightarrow{FC})•(\overrightarrow{AF}-\overrightarrow{FC})={\overrightarrow{AF}}^{2}-{\overrightarrow{FC}}^{2}$=${\overrightarrow{AF}}^{2}-\frac{9}{4}$,
∵${\overrightarrow{AF}}^{2}=(\overrightarrow{AE}+\overrightarrow{EF})^{2}={\overrightarrow{AE}}^{2}+{\overrightarrow{EF}}^{2}+2\overrightarrow{AE}•\overrightarrow{EF}$
=10-6cos∠AEF.
∴当∠AEF=π时,${\overrightarrow{AF}}^{2}$取得最大值16.
∴$\overrightarrow{AC}•\overrightarrow{AD}$的最大值为$\frac{55}{4}$.
点评 本题考查平面向量的数量积运算,考查了向量加法与减法的三角形法则,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)为奇函数,且在R上单调递增 | B. | f(x)为偶函数,且在R上单调递增 | ||
| C. | f(x)为奇函数,且在R上单调递减 | D. | f(x)为偶函数,且在R上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x3+2x<0 | B. | ?x∈[0,+∞),x3+2x<0 | C. | ?x∈(-∞,0),x3+2x≥0 | D. | ?x∈[0,+∞),x3+2x≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com