
| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
分析 根据题中的定义,化简整理得$\overrightarrow{α}$?$\overrightarrow{β}$=$\frac{n}{2}$,$\overrightarrow{β}$?$\overrightarrow{α}$=$\frac{m}{2}$,其中m、n都是整数,两式相乘可得cos2θ夹角的范围,讨论可得m,n,从而得出答案.
解答 解:由题意,可得$\overrightarrow{α}$?$\overrightarrow{β}$=$\frac{\overrightarrow{α}•\overrightarrow{β}}{\overrightarrow{β}•\overrightarrow{β}}$=$\frac{|\overrightarrow{α}|•|\overrightarrow{β}|cosθ}{|\overrightarrow{β}{|}^{2}}$=$\frac{|\overrightarrow{α}|cosθ}{|\overrightarrow{β}|}$=$\frac{n}{2}$,
同理可得$\overrightarrow{β}$?$\overrightarrow{α}$=$\frac{|\overrightarrow{β}|cosθ}{|\overrightarrow{a}|}$=$\frac{m}{2}$,其中m、n都是整数,
将化简的两式相乘,可得cos2θ=$\frac{mn}{4}$,
∵|$\overrightarrow{α}$|≥|$\overrightarrow{β}$|,
∴n≥m 且m、n∈Z,
∵$\overrightarrow{α}$,$\overrightarrow{β}$的夹角θ∈(0,$\frac{π}{4}$),可得cos2θ∈($\frac{1}{2}$,1),
即$\frac{mn}{4}$∈($\frac{1}{2}$,1),结合m、n均为整数,可得m=1且n=3,
从而得$\overrightarrow{α}$?$\overrightarrow{β}$=$\frac{n}{2}$=$\frac{3}{2}$,
故选:B.
点评 本题给出新定义,求式子 $\overrightarrow{α}$?$\overrightarrow{β}$的值.着重考查了向量数量积及其运算性质、三角函数的性质和整数解的讨论等知识,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
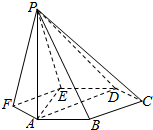 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
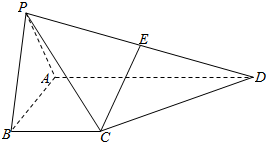 如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.
如图,在四棱锥P-ABCD 中,侧面PAB 为正三角形,侧面PAB⊥底面ABCD,E 为PD 的中点,AB⊥AD,BC∥AD,且AB=BC=$\frac{1}{2}$AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
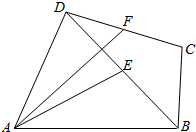 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com