
分析 设抛物线方程为y2=2px(p≠0),将直线方程y=2x-4代入,并整理,利用韦达定理,结合弦长公式,即可求抛物线的方程及它的准线方程.
解答 解:设所求的抛物线方程为 y2=ax (a≠0),A((x1,y1),B(x2,y2)
由y2=ax与y=2x-4,消去y得4x2-( a+16)x+16=0 …(2分)
由△=(a+16)2-256>0得a>0,或a<-32
∵x1+x2=$\frac{a+16}{4}$x1 x2=4 …(4分)
∴|AB|=$\sqrt{(1+{2^2})[{{({x_1}+{x_2})}^2}-4{x_1}•{x_2}]}$=$\sqrt{5[{{(\frac{a+16}{4})}^2}-16]}$
∴$\sqrt{5[{{(\frac{a+16}{4})}^2}-16]}$=45
∴a=4或a=-36 …(8分)
∴所求抛物线方程为y2=4x或y2=-36x …(10分)
准线方程分别为x=-1,x=9 …(12分)
点评 本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查抛物线的弦长计算,属于中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
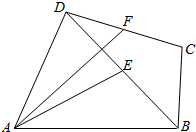 四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.
四边形ABCD中,E,F分别为BD,DC的中点,AE=DC=3,BC=2,BD=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com