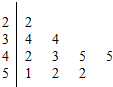Question

9．近日有媒体在全国范围开展“2015年国人年度感受”的调查，在某城市广场有记者随机访问10个步行的路人，其年龄的茎叶图如下：
（1）求这些路人年龄的中位数与方差；
（2）若从40岁以上的路人中，随机抽取3人，其中50岁以上的路人数为X，求X的数学期望．

Answer 1

分析 （1）把茎叶图中的数据按照从小到大的顺序排列，求出中间两个数的平均数即是中位数；再求出这组数据的平均数与方差；
（2）40岁以上有7人，其中40～50岁有4人，50岁以上有3人，X=0，1，2，3，计算对应的概率，即可求X的数学期望．

解答 解：（1）根据茎叶图中的数据，把这10个数据按照从小到大的顺序排列，
排在中间的两个数是43和45，则这组数据的中位数是$\frac{43+45}{2}$=44；
平均数是$\overline{x}$=$\frac{1}{10}$×（22+34+34+42+43+45+45+51+52+52）=42，
方差是s²=$\frac{1}{10}$[（22-42）²+（34-42）²×2+（42-42）²+（43-42）²+（45-42）²×2+（51-42）²+（52-42）²×2=82.8；
（2）40岁以上的路人有7人，其中40～50岁有4人，50岁以上有3人，
X=0，1，2，3．
P（X=0）=$\frac{{C}_{4}^{3}}{{C}_{7}^{3}}$=$\frac{4}{35}$，P（X=1）=$\frac{{C}_{4}^{2}{C}_{3}^{1}}{{C}_{7}^{3}}$=$\frac{18}{35}$，P（X=2）=$\frac{{C}_{4}^{1}{C}_{3}^{2}}{{C}_{7}^{3}}$=$\frac{12}{35}$，P（X=3）=$\frac{1}{35}$．
∴EX=1×$\frac{18}{35}$+2×$\frac{12}{35}$+3×$\frac{1}{35}$=$\frac{9}{7}$．

点评 本题考查了利用茎叶图中的数据求中位数与平均数、考查求X的数学期望，考查学生分析解决问题的能力，属于中档题．