
分析 (1)f(x)在(-∞,0)上为减函数.运用函数的单调性的定义加以证明,注意取值、作差、变形和定符号、下结论几个步骤;
(2)利用不等式恒成立,进行转化求解即可,
(3)利用函数与方程的关系进行转化,利用参数分离法结合数形结合进行讨论即可.
解答 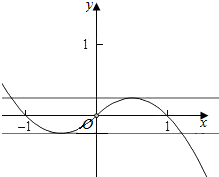 解:(1)由当m=1,且x<0时,f(x)=-x+$\frac{1}{x}$-1是单调递减的.
解:(1)由当m=1,且x<0时,f(x)=-x+$\frac{1}{x}$-1是单调递减的.
证明:设x1<x2<0,则
f(x1)-f(x2)=-x1+$\frac{1}{{x}_{1}}$-1-(-x2+$\frac{1}{{x}_{2}}$-1)=x2-x1+$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$
=(x2-x1)-$\frac{{x}_{1}-{x}_{2}}{{x}_{1}{x}_{2}}$=(x2-x1)(1+$\frac{1}{{x}_{1}{x}_{2}}$),
∵x1<x2<0,则x2-x1>0,x1x2>0,则有f(x1)-f(x2)>0,
f(x1)>f(x2)
则f(x))在(-∞,0)上为减函数;
(2)由 f(log2x)>0得|log2x|+$\frac{m}{lo{g}_{2}x}$-1>0,
当x∈(1,+∞),log2x>0,
则不等式变形为(log2x)2-log2x+m>0,
即m>-(log2x)2+log2x,
而g(x)=-(log2x)2+log2x=-(log2x-$\frac{1}{2}$)2+$\frac{1}{4}$,
当log2x=$\frac{1}{2}$,即x=$\sqrt{2}$时,g(x)取得最大值$\frac{1}{4}$,--------7分
∴m>$\frac{1}{4}$.
(3)由f(x)=0可得x|x|-x+m=0,变为m=-x|x|+x,x≠0
令h(x)=x-x|x|=$\left\{\begin{array}{l}{-{x}^{2}+x,}&{x>0}\\{{x}^{2}+x,}&{x<0}\end{array}\right.$-----9分
作出函数h(x)的图象及直线y=m,由图象可得:
当m>$\frac{1}{4}$或m<-$\frac{1}{4}$时,f(x)有1个零点.-----10分
当m=$\frac{1}{4}$或m=0或m=-$\frac{1}{4}$时,f(x)有2个零点;-----11分
当0<m<$\frac{1}{4}$或-$\frac{1}{4}$<m<0时,f(x)有3个零点.-------12分.
点评 本题考查不等式恒成立以及函数的单调性的判断以及证明,考查函数的零点的判断,考查分类讨论的思想方法,考查运算能力,属于中档题和易错题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
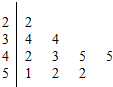 近日有媒体在全国范围开展“2015年国人年度感受”的调查,在某城市广场有记者随机访问10个步行的路人,其年龄的茎叶图如下:
近日有媒体在全国范围开展“2015年国人年度感受”的调查,在某城市广场有记者随机访问10个步行的路人,其年龄的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在无数个实数k使得点F为线段OB的中点 | |
| B. | 存在唯一的实数k使得点F为线段OB的中点 | |
| C. | 不存在实数k使得点F为线段OB的中点 | |
| D. | 以上命题都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com