
分析 过P作PK⊥l(l为抛物线的准线)于K,则|PF|=|PK|,进而问题转化为求|PA|+|PK|的最小值,当P,A,K三点共线时即当P点的纵坐标与A点的纵坐标相同时,|PA|+|PK|最小,把y=1代入抛物线方程求得x,则点P的纵坐标可得,进而求得P的坐标.
解答 解:过P作PK⊥l(l为抛物线的准线)于K,则|PF|=|PK|,
∴|PA|+|PF|=|PA|+|PK|.
∴当P点的纵坐标与A点的纵坐标相同时,
|PA|+|PK|最小,此时P点的纵坐标为1,把y=1代入y2=-4x,得x=-$\frac{1}{4}$,
即当P点的坐标为(-$\frac{1}{4}$,1)时,|PA|+|PF|最小.
故答案为:$(-\frac{1}{4},1)$.
点评 本题主要考查了抛物线的简单性质.考查了学生对抛物线基础知识的掌握和数形结合思想的应用.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
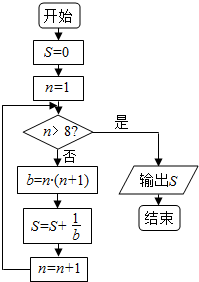
| A. | $\frac{7}{8}$ | B. | $\frac{9}{10}$ | C. | $\frac{8}{9}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
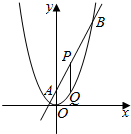 已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com