
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
分析 设出A,B,C三点坐标,求出$\overrightarrow{CA},\overrightarrow{CB}$,根据∠ACB=90°列方程得出三点横坐标的关系得出|CD|,利用相似三角形得出|AD|•|BD|=|CD|2.
解答 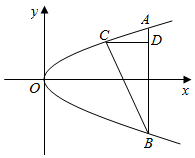 解:设A(4t2,4t),B(4t2,-4t),C(4m2,4m),
解:设A(4t2,4t),B(4t2,-4t),C(4m2,4m),
∴$\overrightarrow{CA}$=(4t2-4m2,4t-4m),$\overrightarrow{CB}$=(4t2-4m2,-4t-4m).
∵∠ACB=90°,∴$\overrightarrow{CA}•\overrightarrow{CB}=0$.
∴16(t2-m2)2-16(t2-m2)=0,∴m2-t2=-1或m2-t2=0(舍).
∴|CD|=4|t2-m2|=4,
在Rt△ABC中,∵CD⊥AB,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴|AD|•|BD|=|CD|2=16.
故选:A.
点评 本题考查了抛物线的性质,直线与抛物线的关系,属于中档题.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
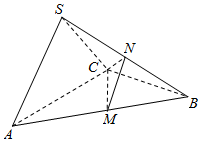 在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.
在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2$\sqrt{3}$,M、N分别为AB,SB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com