Question

2．在公比为2的等比数列{a_n}中，a₂与a₃的等差中项是9$\sqrt{3}$．
（Ⅰ）求a₁的值；
（Ⅱ）若函数y=|a₁|sin（$\frac{π}{4}$x+φ），|φ|＜π，的一部分图象如图所示，M（-1，|a₁|），N（3，-|a₁|）为图象上的两点，设∠MPN=β，其中P与坐标原点O重合，0＜β＜π，求tan（φ-β）的值．

Answer 1

分析 （Ⅰ）根据等比数列和等差数列的性质进行求解即可．
（Ⅱ）根据三角函数的图象确实A，ω和φ的值即可．

解答 解：（Ⅰ） 解：由题可知${a_2}+{a_5}=18\sqrt{3}$，又a₅=8a₂，（3分）
故${a_2}=2\sqrt{3}$，
∴a₁=$\sqrt{3}$  （5分）
（Ⅱ）∵点M（-1，|a₁|），在函数y=|a₁|sin（$\frac{π}{4}$x+φ），|φ|＜π的图象上，
∴sin（-$\frac{π}{4}$+φ）=1，
又∵|φ|＜π，∴φ=$\frac{3π}{4}$   （7分）

如图，连接MN，在△MPN中，由余弦定理得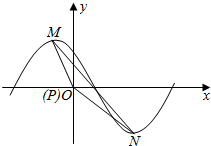

$cosβ=\frac{{{{|{PM}|}^2}+{{|{PN}|}^2}-{{|{MN}|}^2}}}{{2|{PM}||{PN}|}}=\frac{4+12-28}{{8\sqrt{3}}}=-\frac{{\sqrt{3}}}{2}$，
又∵0＜β＜π，∴$β=\frac{5}{6}π$（9分）

∴$ϕ-β=-\frac{π}{12}$，
∴tan（φ-β）=-tan$\frac{π}{12}$=-tan（$\frac{π}{4}$-$\frac{π}{6}$）=-2+$\sqrt{3}$  （12分）

点评 本题主要考查数列与三角函数的综合，根据等比数列和等差数列的性质结合三角函数的图象和性质是解决本题的关键．