设等比数列{an}的前n项和为Sn,a4=a1-9,a5,a3,a4成等差数列.
(1)求数列{an}的通项公式,
(2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
解:(1)设等比数列{a
n}的公比为q,
则

,解得
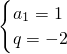
,
故数列{a
n}的通项公式为:a
n=(-2)
n-1,
(2)由(1)可知a
n=(-2)
n-1,
故S
k=
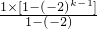
=
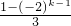
,
所以S
k+1=
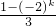
,S
k+2=
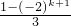
,
∴S
k+1+S
k+2=
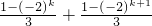
=
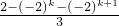
=

=
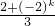
,
而2S
k=2
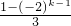
=
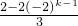
=
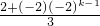
=
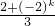
,
故S
k+1+S
k+2=2S
k,即S
k+2,S
k,S
k+1成等差数列
分析:(1)由题意可建立

,解之可得
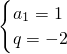
,进而可得通项公式;
(2)由(1)可求S
k,进而可得S
k+2,S
k+1,由等差中项的定义验证S
k+1+S
k+2=2S
k即可
点评:本题考查等比数列的前n项和,以及等差关系的确定,属中档题.
