Question

20．已知半径为1的球O内切于正四面体A-BCD，线段MN是球O的一条动直径（M．N是直径的两端点），点P是正四面体A-BCD的表面上的一个动点，则|${\overrightarrow{PM}$+$\overrightarrow{PN}}$|的取值范围是[2，6]．

Answer 1

分析 运用向量的加减运算的性质：向量的模的定义，讨论P位于切点E和顶点时分别取得最值，即可得到所求取值范围．

解答 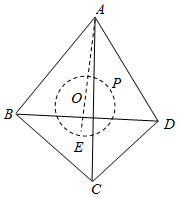解：由题意M，N是直径的两端点，可得$\overrightarrow{OM}$+$\overrightarrow{ON}$=$\overrightarrow{0}$，$\overrightarrow{OM}$•$\overrightarrow{ON}$=-1，
∴|$\overrightarrow{PM}$+$\overrightarrow{PN}$|=|$\overrightarrow{PO}$+$\overrightarrow{OM}$+$\overrightarrow{PO}$+$\overrightarrow{ON}$|=2|$\overrightarrow{PO|}$，
即求正四面体表面上的动点P到O的距离的范围．
当P位于E（切点）时，OP取得最小值1；
当P位于A处时，OP即为正四面体外接球半径最大即为3．
设正四面体的边长为a，由O为正四面体的中心，
可得直角三角形ABE中，AE=$\frac{\sqrt{6}}{3}$a，BE=$\frac{\sqrt{3}}{3}$a，OE=$\frac{\sqrt{6}}{12}$a，AO=$\frac{\sqrt{6}}{4}$a，
综上可得|$\overrightarrow{PO}$|的最小值为1，最大值为3，
则|$\overrightarrow{PM}$+$\overrightarrow{PN}$|的取值范围是[2，6]．
故答案为：[2，6]．

点评 本题考查向量在几何中的运用，考查向量的加减运算的性质，考查运算能力，属于中档题．