练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．若关于x的方程2cos2x+5sinx-4=a有实数解，则实数a的取值范围是[-9，1]．

    分析 令sinx=t，则关于t的方程a=-2t2+5t-2在[-1，1]上有解，求出右侧函数的值域即可得出a的范围．

    解答 解：有2cos2x+5sinx-4=a得-2sin2x+5sinx-2=a，
    令sinx=t，则a=-2t2+5t-2，t∉[-1，1]．
    令f（t）=-2t2+5t-2，则f（t）在[-1，1]上单调递增，
    ∴fmin（t）=f（-1）=-9，fmax（t）=f（1）=1，
    ∵关于x的方程2cos2x+5sinx-4=a有实数解，
    ∴关于t的方程a=-2t2+5t-2在[-1，1]上有解，
    ∴-9≤a≤1．
    故答案为：[-9，1]．

    点评 本题考查了根的存在性问题，函数值域的计算，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

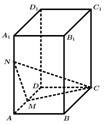    19．如图，在长方体ABCD-A1B1C1D1中，AA1=6，AB=3，AD=8，点M是棱AD的中点，点N在棱AA1上，且满足AN=2NA1，P是侧面四边形ADD1A1内一动点（含边界），若C1P∥平面CMN，则线段C1P长度的取值范围是（　　）
    A．$[{\sqrt{17}，5}]$B．[4，5]C．[3，5]D．$[{3，\sqrt{17}}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为（　　）
    A．[-$\frac{1}{2}$，+∞）B．（-∞，$\frac{3}{4}$]C．[-$\frac{1}{2}$，$\frac{3}{4}$]D．（-$\frac{1}{2}$，$\frac{3}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．若$sin（{-\frac{3}{2}π+α}）＜0$且$cos（{\frac{3}{2}π+α}）＞0$，则α的终边所在的象限为第二象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在四边形ABCD中，∠A=90°，∠B=60°，∠D=120°，对角线AC长为4，则对角线BD的长为$\frac{8\sqrt{3}}{3}$，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若函数$f（x）=\sqrt{3}sin2x+acos2x$的图象关于直线$x=-\frac{π}{8}$对称，则实数a=-$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．在△ABC中，若a=4，b=3，c=2，则△ABC的最小角为arccos$\frac{7}{8}$（用反三角函数表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若动直线x=a与$f（x）=sin（{x+\frac{π}{6}}）$和g（x）=2cosx的图象分别交于M，N两点，则|MN|的最大值为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．化简求值：
    （1）$\sqrt{6\frac{1}{4}}+\sqrt{3\frac{3}{8}}+\sqrt{0.0625}{+（\sqrt{π}）}^{0}{-2}^{-1}$
    （2）lg14-2lg$\frac{7}{3}$+lg7-lg18．

    查看答案和解析>>

    同步练习册答案