练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$的定义域为（　　）
    A．[-$\frac{1}{2}$，+∞）B．（-∞，$\frac{3}{4}$]C．[-$\frac{1}{2}$，$\frac{3}{4}$]D．（-$\frac{1}{2}$，$\frac{3}{4}$）

    分析 根据二次根式被开方数大于或等于0，列出不等式组求出解集即可．

    解答 解：函数y=$\sqrt{2x+1}$+$\sqrt{3-4x}$，
    ∴$\left\{\begin{array}{l}{2x+1≥0}\\{3-4x≥0}\end{array}\right.$，
    解得-$\frac{1}{2}$≤x≤$\frac{3}{4}$，
    ∴函数y的定义域为[-$\frac{1}{2}$，$\frac{3}{4}$]．
    故选：C．

    点评 本题考查了根据函数解析式求定义域的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．若圆C：x2+y2-2x+4y=0上存在两点A，B关于直线l：y=kx-1对称，则k的值为（　　）
    A．-1B．-$\frac{3}{2}$C．-$\frac{5}{2}$D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知△ABC是等腰直角三角形，AC=BC=2，则$\overrightarrow{AB}•\overrightarrow{BC}$=-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．中央电视台有一个非常受欢迎的娱乐节目：墙来了！选手需要按墙上的空调造型摆出相同姿势才能穿墙而过，否则会被墙推入水池，类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空间，则该几何体为（　　）
    A．B．C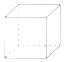．D．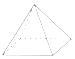

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．在下列条件中：①b2-4ac≥0；②ac＞0；③ab＜0且ac＞0；④b2-4ac≥0，$\frac{b}{a}＜0，\frac{c}{a}$＞0中能成为“使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件是（　　）
    A．①②③B．①②④C．①③④D．②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知直线?1：ax-y-1=0，?2：x+y+3=0，若?1⊥?2，则a 的值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在R上定义运算?：x?y=x（1-y），若存在x1，x2（x1≠x2）使得1?（2k-3-kx）=1+$\sqrt{4-{x^2}}$成立，则实数k的取值范围为（　　）
    A．$（\frac{5}{12}，+∞）$B．$（\frac{5}{12}，\frac{3}{4}]$C．$（0，\frac{5}{12}）$D．$（\frac{1}{3}，\frac{3}{4}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若关于x的方程2cos2x+5sinx-4=a有实数解，则实数a的取值范围是[-9，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知f（x）是定义在R上的偶函数，并且有$f（x+2）=\frac{1}{f（x）}$，当2≤x≤3时，f（x）=x，则f（105.5）=2.5．

    查看答案和解析>>

    同步练习册答案