
分析 由已知得AB=2$\sqrt{2}$,<$\overrightarrow{AB}•\overrightarrow{BC}$>=1350,$\overrightarrow{AB}•\overrightarrow{BC}$=|$\overrightarrow{AB}$|×|$\overrightarrow{BC}$|cos135°,代入计算即可得到所求值.
解答 解:∵△ABC是等腰直角三角形,AC=BC=2,∴AB=2$\sqrt{2}$,<$\overrightarrow{AB}•\overrightarrow{BC}$>=1350,
$\overrightarrow{AB}•\overrightarrow{BC}$=|$\overrightarrow{AB}$|×|$\overrightarrow{BC}$|cos135°=2$\sqrt{2}$×2×(-$\frac{\sqrt{2}}{2}$)=-4
故答案为:-4
点评 本题考查了向量的数量积运算,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
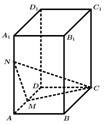 如图,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )
如图,在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度的取值范围是( )| A. | $[{\sqrt{17},5}]$ | B. | [4,5] | C. | [3,5] | D. | $[{3,\sqrt{17}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
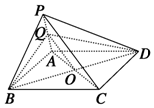
| A. | OQ∥平面PCD | B. | PC∥平面BDQ | C. | AQ∥平面PCD | D. | CD∥平面PAB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,+∞) | B. | (-∞,$\frac{3}{4}$] | C. | [-$\frac{1}{2}$,$\frac{3}{4}$] | D. | (-$\frac{1}{2}$,$\frac{3}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com