
【题目】已知椭圆![]() :在
:在![]() 轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为
轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() ,
,![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() ,
,![]() 分别和圆
分别和圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】为测试特斯拉汽车的百米加速时间,研发人员记录了汽车在![]() 取
取![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时刻的位移,并对数据做了初步处理,得到图
时刻的位移,并对数据做了初步处理,得到图![]() .同时,令
.同时,令![]() ,得到数据图
,得到数据图![]() ,现画出
,现画出![]() 与
与![]() ,
,![]() 与
与![]() 的散点图.
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|

(1)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪两个量之间线性相关程度更强?(直接给出判断即可);
哪两个量之间线性相关程度更强?(直接给出判断即可);
(2)根据(1)的结果选择线性相关程度更强的两个量,建立相应的回归直线方程;
(3)根据(2)的结果预计特斯拉汽车百米加速需要的时间.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有12支球队进行足球比赛,每两队都赛一场,胜者得3分,负者得0分,平局各得1分那么,有1支球队最少要得多少分才能保证最多有6支球队的得分不少于该队的得分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98,请估计该等级的中国小龙虾销售单价为多少元?
参考公式:对一组数据![]() ,
,![]() ,····
,····![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: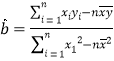 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数.f(t),随时刻t(时)变化的规律满足表达式![]() ,其中a为空气治理调节参数,且a∈(0,1).
,其中a为空气治理调节参数,且a∈(0,1).
(1)令![]() ,求x的取值范围;
,求x的取值范围;
(2)若规定每天中f(t)的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:“幂势既同,则积不容异”,“势”即是高,“幂”是面积.意思是,如果夹在两平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都是h),其中:三棱锥的体积为V,四棱锥的底面是边长为a的正方形,圆锥的底面半径为r,现用平行于这两个平面的平面去截三个几何体,如果得到的三个截面面积总相等,那么,下面关系式正确的是( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
(1)求证:直线MN必过定点;
(2)分别以AB和CD为直径作圆,求两圆相交弦中点H的轨迹方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com