
【题目】为测试特斯拉汽车的百米加速时间,研发人员记录了汽车在![]() 取
取![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时刻的位移,并对数据做了初步处理,得到图
时刻的位移,并对数据做了初步处理,得到图![]() .同时,令
.同时,令![]() ,得到数据图
,得到数据图![]() ,现画出
,现画出![]() 与
与![]() ,
,![]() 与
与![]() 的散点图.
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|

(1)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪两个量之间线性相关程度更强?(直接给出判断即可);
哪两个量之间线性相关程度更强?(直接给出判断即可);
(2)根据(1)的结果选择线性相关程度更强的两个量,建立相应的回归直线方程;
(3)根据(2)的结果预计特斯拉汽车百米加速需要的时间.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
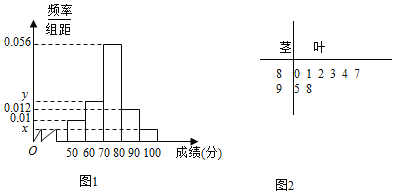
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用![]() 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为![]() 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:厘米)满足关系:
(单位:厘米)满足关系:![]() .若不建隔热层,每年的能源消耗费用为
.若不建隔热层,每年的能源消耗费用为![]() 万元.设
万元.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 最小,并求其最小值.
最小,并求其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 在区间
在区间![]() 上的最小值和最大值;
上的最小值和最大值;
(3)若![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y2=4x的焦点为F,抛物线上有三个动点A,B,C.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,AB的垂直平分线经过一个定点Q,求△QAB面积的最大值.
,AB的垂直平分线经过一个定点Q,求△QAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象相邻两条对称轴的距离为
图象相邻两条对称轴的距离为![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到的图象关于y轴对称则函数
个单位后,得到的图象关于y轴对称则函数![]() 的图象( )
的图象( )
A. 关于直线![]() 对称 B. 关于直线
对称 B. 关于直线![]() 对称
对称
C. 关于点![]() 对称 D. 关于点
对称 D. 关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() .椭圆C的长轴与焦距之比为
.椭圆C的长轴与焦距之比为![]() ,过
,过![]() 的直线l与C交于A、B两点.
的直线l与C交于A、B两点.
(1)求椭圆的方程;
(2)当l的斜率为1时,求![]() 的面积;
的面积;
(3)当线段![]() 的垂直平分线在y轴上的截距最小时,求直线l的方程.
的垂直平分线在y轴上的截距最小时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :在
:在![]() 轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为
轴上的一个焦点,与短轴两个端点的连线互相垂直,且右焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() ,
,![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() ,
,![]() 分别和圆
分别和圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com