
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() .椭圆C的长轴与焦距之比为
.椭圆C的长轴与焦距之比为![]() ,过
,过![]() 的直线l与C交于A、B两点.
的直线l与C交于A、B两点.
(1)求椭圆的方程;
(2)当l的斜率为1时,求![]() 的面积;
的面积;
(3)当线段![]() 的垂直平分线在y轴上的截距最小时,求直线l的方程.
的垂直平分线在y轴上的截距最小时,求直线l的方程.
【答案】(1)![]() (2)12(3)
(2)12(3)![]() .
.
【解析】
(1)根据已知条件求得![]() ,由此求得椭圆方程.
,由此求得椭圆方程.
(2)求得直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,求得
的方程和椭圆方程,求得![]() 两点的纵坐标,由此求得三角形
两点的纵坐标,由此求得三角形![]() 的面积.
的面积.
(3)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和抛物线方程,化简后写出韦达定理,求得线段
的方程和抛物线方程,化简后写出韦达定理,求得线段![]() 中点
中点![]() 的坐标,设线段
的坐标,设线段![]() 的垂直平分线与y轴的交点为
的垂直平分线与y轴的交点为![]() ,根据
,根据![]() 求得
求得![]() 关于
关于![]() 的表达式,由此求得
的表达式,由此求得![]() 的最小值,以及此时
的最小值,以及此时![]() 的值,进而求得直线
的值,进而求得直线![]() 的方程.
的方程.
(1)依题意,因![]() ,又
,又![]() ,得
,得![]() ,
,![]()
所以椭圆C的方程为![]() .
.
(2)设![]() 、
、![]() ,当
,当![]() 时,直线l:
时,直线l:![]() ,将直线与椭圆方程联立
,将直线与椭圆方程联立 ,消去x得,
,消去x得,![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
(3)设直线l的斜率为k,由题意可知![]() ,由
,由 ,消去y得
,消去y得![]() ,
,![]() 恒成立,
恒成立,![]() ,
,
设线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,![]() ,
,
设线段![]() 的垂直平分线与y轴的交点为
的垂直平分线与y轴的交点为![]() ,则
,则![]() ,得
,得 .
.
![]() ,整理得:
,整理得:![]() ,
, ,等号成立时
,等号成立时![]() .故当截距m最小为
.故当截距m最小为![]() 时,
时,![]() ,此时直线l的方程为
,此时直线l的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为测试特斯拉汽车的百米加速时间,研发人员记录了汽车在![]() 取
取![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时刻的位移,并对数据做了初步处理,得到图
时刻的位移,并对数据做了初步处理,得到图![]() .同时,令
.同时,令![]() ,得到数据图
,得到数据图![]() ,现画出
,现画出![]() 与
与![]() ,
,![]() 与
与![]() 的散点图.
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|

(1)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪两个量之间线性相关程度更强?(直接给出判断即可);
哪两个量之间线性相关程度更强?(直接给出判断即可);
(2)根据(1)的结果选择线性相关程度更强的两个量,建立相应的回归直线方程;
(3)根据(2)的结果预计特斯拉汽车百米加速需要的时间.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间四边形ABCD,∠BAC=![]() ,AB=AC=2
,AB=AC=2![]() ,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
,BD=CD=6,且平面ABC⊥平面BCD,则空间四边形ABCD的外接球的表面积为( )
A. 60π B. 36π C. 24π D. 12π
查看答案和解析>>
科目:高中数学 来源: 题型:
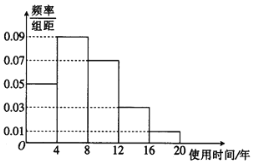
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
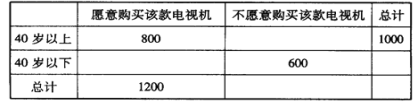
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有12支球队进行足球比赛,每两队都赛一场,胜者得3分,负者得0分,平局各得1分那么,有1支球队最少要得多少分才能保证最多有6支球队的得分不少于该队的得分?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:“幂势既同,则积不容异”,“势”即是高,“幂”是面积.意思是,如果夹在两平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都是h),其中:三棱锥的体积为V,四棱锥的底面是边长为a的正方形,圆锥的底面半径为r,现用平行于这两个平面的平面去截三个几何体,如果得到的三个截面面积总相等,那么,下面关系式正确的是( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com