
【题目】已知二次函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 在区间
在区间![]() 上的最小值和最大值;
上的最小值和最大值;
(3)若![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)因为![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,即可求得答案;
上单调递减,即可求得答案;
(2)![]() ,其对称轴为
,其对称轴为![]() 且图象开口向上,又因为
且图象开口向上,又因为![]() 在区间
在区间![]() 上是减函数,根据二次函数图象可得:
上是减函数,根据二次函数图象可得:![]() ,故
,故![]() (注:
(注:![]() 更接近对称轴为
更接近对称轴为![]() ),即可求得答案;
),即可求得答案;
(3)因为![]() 在区间
在区间![]() 上有零点,分别讨论
上有零点,分别讨论![]() 和
和![]() ,即可求得答案.
,即可求得答案.
(1)![]()
![]()
可化简为:![]() ,
,
根据二次函数知识可得:![]() 其对称轴为
其对称轴为![]()
![]()
![]() 在
在![]() 上单调递减,
上单调递减,
则有![]() ,即
,即![]()
解得:![]()
(2)![]()
![]() ,其对称轴为
,其对称轴为![]() 且图象开口向上
且图象开口向上
又![]()
![]() 在区间
在区间![]() 上是减函数
上是减函数
根据二次函数图像可得:![]() ,
,
![]()
![]() (注:
(注:![]() 更接近对称轴为
更接近对称轴为![]() )
)
又![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增:
上单调递增:
![]()
![]()
(3)①当![]() 时,
时,![]()
![]()
![]() ,其对称轴为
,其对称轴为![]() 且图象开口向上
且图象开口向上
![]()
![]() 在区间
在区间![]() 是减函数
是减函数
![]()
![]() ,
,
则![]() 在区间
在区间![]() 上无零点;
上无零点;
②当![]() 时,
时,![]() 且
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]()
![]() ,
,
即![]()
由上述知:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
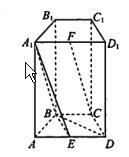
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4张牌(如图)每张牌的一面都写上一个英文字母,另一面都写上一个数字.规定:当牌的一面为字母![]() 时,它的另一面必须写数字2.你的任务是:为了检验下面的4张牌是否有违反规定的写法,你翻看哪几张牌就够了.你的选择是( ).
时,它的另一面必须写数字2.你的任务是:为了检验下面的4张牌是否有违反规定的写法,你翻看哪几张牌就够了.你的选择是( ).
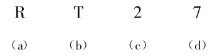
A. ![]() B.
B. ![]() 、
、![]()
C. ![]() 、
、![]() D. 非以上答案
D. 非以上答案
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为测试特斯拉汽车的百米加速时间,研发人员记录了汽车在![]() 取
取![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时刻的位移,并对数据做了初步处理,得到图
时刻的位移,并对数据做了初步处理,得到图![]() .同时,令
.同时,令![]() ,得到数据图
,得到数据图![]() ,现画出
,现画出![]() 与
与![]() ,
,![]() 与
与![]() 的散点图.
的散点图.
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
累加 |
|
|
|
| 累加 |
|
|
|
|

(1)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪两个量之间线性相关程度更强?(直接给出判断即可);
哪两个量之间线性相关程度更强?(直接给出判断即可);
(2)根据(1)的结果选择线性相关程度更强的两个量,建立相应的回归直线方程;
(3)根据(2)的结果预计特斯拉汽车百米加速需要的时间.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,“六芒星”是由两个全等正三角形组成,中心重合于点![]() 且三组对边分别平行,点
且三组对边分别平行,点![]() 是“六芒星”(如图)的两个顶点,动点
是“六芒星”(如图)的两个顶点,动点![]() 在“六芒星”上(内部以及边界),若
在“六芒星”上(内部以及边界),若![]() ,则
,则![]() 的取值可能是( )
的取值可能是( )
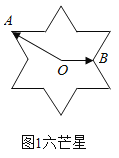
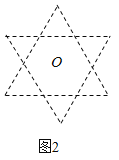
A.![]() B.1C.5D.9
B.1C.5D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com