
【题目】有4张牌(如图)每张牌的一面都写上一个英文字母,另一面都写上一个数字.规定:当牌的一面为字母![]() 时,它的另一面必须写数字2.你的任务是:为了检验下面的4张牌是否有违反规定的写法,你翻看哪几张牌就够了.你的选择是( ).
时,它的另一面必须写数字2.你的任务是:为了检验下面的4张牌是否有违反规定的写法,你翻看哪几张牌就够了.你的选择是( ).
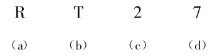
A. ![]() B.
B. ![]() 、
、![]()
C. ![]() 、
、![]() D. 非以上答案
D. 非以上答案
【答案】C
【解析】
思路1:逐一翻每张牌,设想背面的各种可能,可得出![]() 、
、![]() 不用翻.为了帮助理解,可设想十字路口上“红灯亮了”代表“一面写上英文字母
不用翻.为了帮助理解,可设想十字路口上“红灯亮了”代表“一面写上英文字母![]() ”,而把“行人不过马路”代表“另一面写上数字2”,检验是否违反规定,就成为检验是否“红灯亮时,行人过马路”违反交通规则(红灯不亮时,过不过马路都不违反交通规则).
”,而把“行人不过马路”代表“另一面写上数字2”,检验是否违反规定,就成为检验是否“红灯亮时,行人过马路”违反交通规则(红灯不亮时,过不过马路都不违反交通规则).
思路2:把“规定”理解为:假言推理“若![]() 则
则![]() ”是真命题,
”是真命题,![]() 真代表“一面写上英文字母
真代表“一面写上英文字母![]() ”,
”,![]() 真代表“另一面写上数字2”.由真值表可见:
真代表“另一面写上数字2”.由真值表可见:
|
|
|
真 | 真 | 真 |
真 | 假 | 假 |
假 | 真 | 真 |
假 | 假 | 假 |
(1)当![]() 真时,依
真时,依![]() 的真假,
的真假,![]() 可真可假,故翻看
可真可假,故翻看![]() 是必要的.
是必要的.
(2)当![]() 假时,无论
假时,无论![]() 是真是假,
是真是假,![]() 恒为真,翻看
恒为真,翻看![]() 是多余的.
是多余的.
(3)当![]() 真时,无论
真时,无论![]() 是真是假,
是真是假,![]() 恒为真,翻看
恒为真,翻看![]() 是多余的.
是多余的.
(4)当![]() 假时,依
假时,依![]() 的真假,
的真假,![]() 可真可假,故翻看
可真可假,故翻看![]() 是必要的.
是必要的.
故应翻![]() 、
、![]() .选C.
.选C.
评析:此题除了上面介绍的两种求解思路外,还可以从四种命题或充要条件的角度去理解,甚至直接将“![]() ”代表一个具体数学命题(充分不必要).
”代表一个具体数学命题(充分不必要).


科目:高中数学 来源: 题型:
【题目】已知三棱锥P—ABC中,PC![]() 底面ABC,AB=BC,D、F分别为AC、PC的中点,DE
底面ABC,AB=BC,D、F分别为AC、PC的中点,DE![]() AP于E。(1)求证:AP
AP于E。(1)求证:AP![]() 平面BDE;(2)求证:平面BDE
平面BDE;(2)求证:平面BDE![]() 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四个函数![]() ,其中
,其中![]() ,
,![]() 的图像如图所示.
的图像如图所示.

(1)请在坐标系中画出![]() ,
,![]() 的图像,并根据这四个函数的图像总结出指数函数具有哪些性质?
的图像,并根据这四个函数的图像总结出指数函数具有哪些性质?
(2)举出在实际情境中能够抽象出指数函数的一个例子并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上是减函数,求
上是减函数,求![]() 在区间
在区间![]() 上的最小值和最大值;
上的最小值和最大值;
(3)若![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作之一,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积![]() (弦
(弦![]() 矢
矢![]() 矢
矢![]() ),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
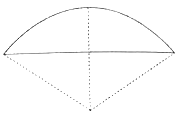
A.12平方米B.16平方米C.20平方米D.24平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
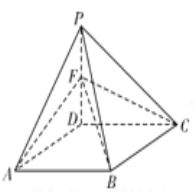
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com