
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出a的值即可;
(2)求出$\frac{a{(e}^{{2x}_{2}}{-e}^{{2x}_{1}})}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$+b-$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$=0,得到2a${e}^{{{x}_{1}+x}_{2}}$+b${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$<$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$•${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$(1),通过换元法求出函数的单调性,证明不等式成立即可.
解答 解:(1)y′=a+$\frac{1}{x}$,x∈(0,e],
若a≥-$\frac{1}{e}$,则x∈(0,e]时,y′≥0,函数y=ax+lnx是递增函数,
ymax=ae+lne=ae+1≥0,不合题意;
若a<-$\frac{1}{e}$,则x∈(0,-$\frac{1}{a}$)时,y′>0,函数y=ax+lnx是递增函数,
则x∈(-$\frac{1}{a}$,e)时,y′<0,函数y=ax+lnx是减函数,
故ymax=-1+ln(-$\frac{1}{a}$)=-4,得a=-e3<-$\frac{1}{e}$,
故a=-e3;
(2)∵x1,x2是函数y=ag(2x)+bg(x)-x的两个不同的零点,
不妨设x1<x2,则a${e}^{{2x}_{1}}$+b${e}^{{x}_{1}}$-x1=0,a${e}^{{2x}_{2}}$+b${e}^{{x}_{2}}$-x2=0,
两式相减得a(${e}^{{2x}_{2}}$-${e}^{{2x}_{1}}$)+b(${e}^{{x}_{2}}$-${e}^{{x}_{1}}$)-(x2-x1)=0,
即$\frac{a{(e}^{{2x}_{2}}{-e}^{{2x}_{1}})}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$+b-$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$=0,
a(${e}^{{x}_{2}}$+${e}^{{x}_{1}}$)+b=$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$,
又${e}^{{x}_{2}}$+${e}^{{x}_{1}}$>2$\sqrt{{{e}^{{x}_{2}}e}^{{x}_{1}}}$=2${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$,
则2a${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$+b<$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$,即2a${e}^{{{x}_{1}+x}_{2}}$+b${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$<$\frac{{x}_{2}{-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$•${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$(1),
令t=x2-x1>0,函数G(t)=${e}^{\frac{t}{2}}$-${e}^{-\frac{t}{2}}$-t,
则G′(t)=$\frac{1}{2}$${e}^{\frac{t}{2}}$+$\frac{1}{2}$${e}^{-\frac{t}{2}}$-1>0,函数G(t)在(0,+∞)递增,
G(t)>G(0)=0,
故${e}^{\frac{{{x}_{2}-x}_{1}}{2}}$-${e}^{-\frac{{{x}_{2}-x}_{1}}{2}}$-(x2-x1)>0,即$\frac{{{x}_{2}-x}_{1}}{{{e}^{\frac{{{x}_{2}-x}_{1}}{2}}-e}^{-\frac{{x}_{2}{-x}_{1}}{2}}}$<1(2),
又$\frac{{{x}_{2}-x}_{1}}{{{e}^{{x}_{2}}-e}^{{x}_{1}}}$•${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$=$\frac{{{x}_{2}-x}_{1}}{{e}^{{{x}_{2}-x}_{1}}-1}$•${e}^{\frac{{{x}_{2}-x}_{1}}{2}}$=$\frac{{{x}_{2}-x}_{1}}{{{e}^{\frac{{{x}_{2}-x}_{1}}{2}}-e}^{-\frac{{{x}_{2}-x}_{1}}{2}}}$(3),
又∵2ag(2x0)+bg(x0)=2a${e}^{{{x}_{1}+x}_{2}}$+b${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$,
根据(1),(2),(3),
显然不等式2ag(2x0)+bg(x0)<f(e)成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
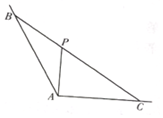 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8\sqrt{3}}{9}$ | B. | $\frac{16\sqrt{3}}{9}$ | C. | $\frac{32\sqrt{3}}{9}$ | D. | $\frac{64\sqrt{3}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
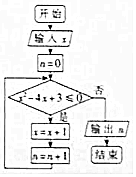 执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )
执行如图所示的程序框图,若输入x的值为1,输出n的值为N,则在区间[-1,4]上随机选取一个数M,M≥N-1的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com