Question

【题目】已知圆：．

（Ⅰ）求过点的圆的切线方程；

（Ⅱ）设圆与轴相交于，两点，点为圆上异于，的任意一点，直线，分别与直线交于，两点．

（ⅰ）当点的坐标为时，求以为直径的圆的圆心坐标及半径；

（ⅱ）当点在圆上运动时，以为直径的圆被轴截得的弦长是否为定值？请说明理由．

Answer 1

【答案】（Ⅰ）或；（Ⅱ）（ⅰ）圆心为，半径；（ⅱ）见解析

【解析】

（Ⅰ）先判断在圆外， 所以圆过点的切线有两条．再由斜率是否存在分别讨论．（Ⅱ）（ⅰ）设直线PA和PB把其与直线交于，两点表示出来，写出圆的方程化简即可．（ⅱ）先求出以为直径的圆被轴截得的弦长，在设出PA和PB的直线方程，分别求出与直线的交点，求出圆心，再根据勾股定理易求解．

（Ⅰ）因为点在圆外， 所以圆过点的切线有两条．

当直线的斜率不存在时，直线方程为，满足条件．

当直线的斜率存在时，可设为，即．

由圆心到切线的距离，解得． 此时切线方程为．

综上，圆的切线方程为或．

（Ⅱ）因为圆与轴相交于，两点，所以，．

（ⅰ）当点坐标为时，直线的斜率为，直线的方程为．

直线与直线的交点坐标为 ，

同理直线的斜率为，直线的方程为．

直线与直线的交点坐标为． 所以以为直径的圆的圆心为，半径．

（ⅱ）以为直径的圆被轴截得的弦长为定值．

设点，则．

直线的斜率为，直线的方程为．

直线与直线的交点坐标为．

同理直线的斜率为，直线的方程为．

直线与直线的交点坐标为．

所以圆的圆心，半径为．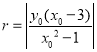

方法一：圆被轴截得的弦长为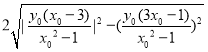

．

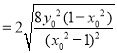
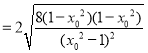
所以以为直径的圆被轴截得的弦长为定值．

方法二：圆的方程为．

令，解得．

所以．

所以圆与轴的交点坐标分别为，．

所以以为直径的圆被轴截得的弦长为定值．