练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知集合A={x|ax2-3x-4=0，x∈R}，若A中至多有一个元素，求实数a的取值范围．

    分析 通过讨论当a=0时，当a≠0时的情况，结合二次函数的性质求出实数a的取值范围．

    解答 解：当a=0时，方程为-3x-4=0，
    ∴集合A={-$\frac{4}{3}$}；
    当a≠0时，若关于x的方程ax2-3x-4=0有两个相等的实数根，
    则A也只有一个元素，此时a=-$\frac{9}{16}$；
    若关于x的方程ax2-3x-4=0没有实数根，
    则A没有元素，此时a＜-$\frac{9}{16}$，
    综合知此时所求的范围是{a|a≤-$\frac{9}{16}$，或a=0}．

    点评 本题考查实数a的取值范围的求法．解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化，注意分类讨论思想的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

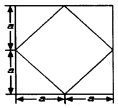    4．已知某个几何体的正视图、侧视图、俯视图均为右图的形状，根据图中标出的尺寸（图中大正方形边长为2a），可得这个几何体的体积是（　　）
    A．$\frac{20}{3}{a^3}$B．7a3C．$2\sqrt{2}{a^3}$D．5a3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设F1，F2分别是椭圆：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|=$\frac{4}{3}$a．则该椭圆的离心率为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=x2-（a+2）x+alnx（a＞0）．
    （Ⅰ）求函数f（x）的单调增区间；
    （Ⅱ）若a=4，y=f（x）的图象与直线y=m有三个不同交点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．下列命题为真命题的是（　　）
    A．?x∈N，x3＞x2
    B．函数f（x）=ax2+bx+c为偶函数的充要条件是b=0
    C．?x0∈R，x02+2x0+2≤0
    D．“x＞3”是“x2＞9”的必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知函数$f（x）=\left\{{\begin{array}{l}{{x^2}+1}&{（x≤0）}\\{-2x}&{（x＞0）}\end{array}}\right.$，则f（3）=6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知定义在R上的奇函数f（x），对任意的实数x都有f（1+x）=f（1-x），且f（-1）=2，则f（4）+f（5）=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．下列说法中错误的是①④（填序号）
    ①命题“?x1，x2∈M，x1≠x2，有[f（x1）-f（x2）]（x2-x1）＞0”的否定是“?x1，x2∉M，x1≠x2，有[f（x1）-f（x2）]（x2-x1）≤0”；
    ②已知a＞0，b＞0，a+b=1，则$\frac{2}{a}$+$\frac{3}{b}$的最小值为5+2$\sqrt{6}$；
    ③设x，y∈R，命题“若xy=0，则x2+y2=0”的否命题是真命题；
    ④已知p：x2+2x-3＞0，q：$\frac{1}{3-x}$＞1，若命题（￢q）∧p为真命题，则x的取值范围是（-∞，-3）∪（1，2）∪[3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．命题“若a＞b，则a-1＞b-1”的逆否命题是若“a-1≤b-1，则a≤b”．

    查看答案和解析>>

    同步练习册答案