
| A. | ?x∈N,x3>x2 | |
| B. | 函数f(x)=ax2+bx+c为偶函数的充要条件是b=0 | |
| C. | ?x0∈R,x02+2x0+2≤0 | |
| D. | “x>3”是“x2>9”的必要条件 |
分析 由x=0,1可得x3=x2,即可判断A;由偶函数的定义和充分必要条件的定义,可判断B;
由配方法和非负数,即可判断C;由充分必要条件的定义和不等式的解法即可判断D.
解答 解:对于A,当x=0或1时,x3=x2=0或1,则?x∈N,x3>x2为假命题;
对于B,函数f(x)=ax2+bx+c为偶函数,可得f(-x)=f(x),求得b=0,反之b=0,可得f(x)为偶函数
故充要条件是b=0,则B为真命题;
对于C,x02+2x0+2=(x0+1)2+1>0,则?x0∈R,x02+2x0+2≤0为假命题;
对于D,“x>3”是“x2>9?x>3或x<-3”的充分条件,故为假命题.
故选:B.
点评 本题考查命题的真假判断,主要考查充分必要条件的判断和全称命题和特称命题的真假,注意运用定义法和反例法,考查判断能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | 32 | B. | 32$\sqrt{2}$ | C. | $\frac{32}{3}$ | D. | $\frac{32}{3}$$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{3}}{5}$ | B. | $\sqrt{15}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
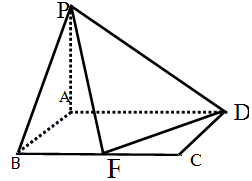 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若l∥m,l?α,则α∥β | ||
| C. | 若m∥l,m∥α,则l∥α | D. | 若α⊥γ,β⊥γ,α∩β=l,则l⊥γ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com