
| 利润x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| Z=2ln(y) | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
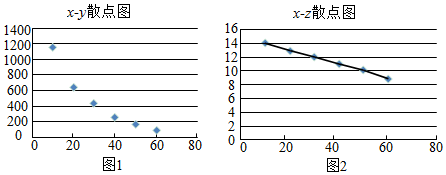
分析 (Ⅰ)根据散点图得出,z与x对应的散点图基本都在一条直线附近,线性相关性更强些;
(Ⅱ)根据公式计算出回归方程的系数,即可写出回归方程;
(Ⅲ)根据回归方程求出年利润函数p=xy,利用导数求出函数p取最大值时x的值即可.
解答 解:(Ⅰ)根据散点图判断,z与x对应的散点图基本都在一条直线附近,
相对y与x具有较强的线性相关性;
(Ⅱ)∵$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{i=6}{(x}_{i}-\overline{x})•{(z}_{i}-\overline{z})}{{\sum_{i=1}^{i=6}{(x}_{i}-\overline{x})}^{2}}$=$\frac{-175.5}{1750}$≈-0.10,
∴$\stackrel{∧}{a}$=$\overline{z}$-$\stackrel{∧}{b}$•$\overline{x}$=11.55-(-0.10)×35=15.05≈15,
即z关于x的回归方程是z=-0.10x+15;
(Ⅲ)∵z=2lny,
∴y=${e}^{\frac{z}{2}}$=${e}^{\frac{-0.10x+15}{2}}$,
∴年利润函数p=xy=x•${e}^{\frac{-0.10x+15}{2}}$,
求导得p′=${e}^{\frac{-0.10x+15}{2}}$(1-$\frac{0.10}{2}$x),
令p′=0,解得x=20;
∴当0<x<20时,P′>0,函数p是单调增函数,
当x>20时,P′<0,函数p是单调减函数,
∴当x=20时年利润函数p的值最大,
即利润为20元/kg时,年利润的预报值最大.
点评 本题考查了求线性回归方程的应用问题,也考查了导数的简单应用问题,是综合性题目.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
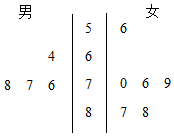 一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| t | 30 | 40 | p | 50 | 70 |
| m | 2 | 4 | 5 | 6 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
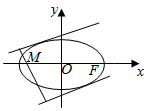 已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.
已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com