
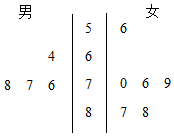
 一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.分析 (Ⅰ)设这10名同学中男女生的平均成绩分别为$\overline{x_1},\overline{x_2}$.利用茎叶图能求出该班男、女生国学素养测试的平均成绩.
(Ⅱ)女生国学素养测试成绩的方差大于男生国学素养成绩的方差.
(Ⅲ)设“两名同学的成绩均为优良”为事件A,男生按成绩由低到高依次编号为a1,a2,a3,a4,女生按成绩由低到高依次编号为b1,b2,b3,b4,b5,b6,由此利用列举法能求出这两名同学的国学素养测试成绩均为优良的概率.
解答 解:(Ⅰ)设这10名同学中男女生的平均成绩分别为$\overline{x_1},\overline{x_2}$.
则$\overline{x_1}=\frac{64+76+77+78}{4}=73.75$….(2分)
$\overline{x_2}=\frac{56+79+76+70++88+87}{6}=76$….
∴该班男、女生国学素养测试的平均成绩分别为73.75,76.(4分)
(Ⅱ)女生国学素养测试成绩的方差大于男生国学素养成绩的方差.….(7分)
(Ⅲ)设“两名同学的成绩均为优良”为事件A,….(8分)
男生按成绩由低到高依次编号为a1,a2,a3,a4,
女生按成绩由低到高依次编号为b1,b2,b3,b4,b5,b6,
则从10名学生中随机选取一男一女两名同学共有24种取法 ….(10分)
(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a1,b5),(a1,b6),(a2,b1),
(a2,b2),(a2,b3),(a2,b4),(a2,b5),(a2,b6),(a3,b1),(a3,b2),
(a3,b3),(a3,b4),(a3,b5),(a3,b6),(a4,b1),(a4,b2),(a4,b3),
(a4,b4),(a4,b5),(a4,b6),
其中两名同学均为优良的取法有12种取法….(12分)
(a2,b3),(a2,b4),(a2,b5),(a2,b6),(a3,b3),(a3,b4),(a3,b5),
(a3,b6),(a4,b2),(a4,b3),(a4,b4),(a4,b5),(a4,b6),
所以$P(A)=\frac{12}{24}=\frac{1}{2}$,
即两名同学成绩均为优良的概率为$\frac{1}{2}$.….(13分)
点评 本题考查茎叶图的应用和概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-5=0 | B. | 2x+y-7=0 | C. | x-2y-5=0 | D. | x-2y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
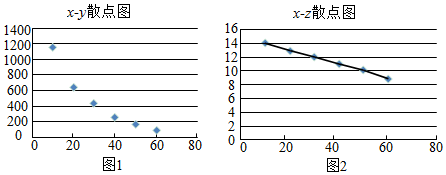
| 利润x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| Z=2ln(y) | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com