
分析 (1)由双曲线D与椭圆C有相同的焦点,且它们的离心率互为倒数,设双曲线D的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),并能求出a,b,从而能求出双曲线D的方程.
(2)①设直线OM为:y=$\sqrt{3}x$,则直线ON为:y=-$\frac{\sqrt{3}}{3}x$,分别与椭圆联立,得到|OM|=3,|ON|=$\sqrt{6}$,由此能求出△MON的面积.
②设P(xP,yP),M(x1,y1),N(x2,y2),则$\left\{\begin{array}{l}{{x}_{P}={x}_{1}+\sqrt{3}{x}_{2}}\\{{y}_{P}={y}_{1}+\sqrt{3}{y}_{2}}\end{array}\right.$,由直线OM与ON的斜率之积为-$\frac{1}{3}$,得x1x2+3y1y2=0,由此能证明动点P在定曲线$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{6}=1$上.
解答 解:(1)∵椭圆C的方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1,
双曲线D与椭圆C有相同的焦点,且它们的离心率互为倒数,
∴设双曲线D的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
且$\left\{\begin{array}{l}{c=\sqrt{9-3}=\sqrt{6}}\\{\frac{c}{a}=\frac{3}{\sqrt{6}}}\\{{c}^{2}={a}^{2}+{b}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{2}$,
∴双曲线D的方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{2}$=1.
(2)①∵M,N是椭圆C上的点,直线OM的斜率为$\sqrt{3}$,且OM⊥ON,
∴设直线OM为:y=$\sqrt{3}x$,则直线ON为:y=-$\frac{\sqrt{3}}{3}x$,
联立$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得${x}^{2}=\frac{9}{10}$,y2=$\frac{81}{10}$,|OM|=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{\frac{9}{10}+\frac{81}{10}}$=3,
联立$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得${x}^{2}=\frac{9}{2}$,y2=$\frac{3}{2}$,|ON|=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{\frac{9}{2}+\frac{3}{2}}$=$\sqrt{6}$,
∴△MON的面积S=$\frac{1}{2}×|OM|×|ON|$=$\frac{3\sqrt{6}}{2}$.
证明:②设P(xP,yP),M(x1,y1),N(x2,y2),
∵$\overrightarrow{OP}$=$\overrightarrow{OM}$$+\sqrt{3}\overrightarrow{ON}$,∴$\left\{\begin{array}{l}{{x}_{P}={x}_{1}+\sqrt{3}{x}_{2}}\\{{y}_{P}={y}_{1}+\sqrt{3}{y}_{2}}\end{array}\right.$,①
由直线OM与ON的斜率之积为-$\frac{1}{3}$,
得:$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{3}$,即x1x2+3y1y2=0,②
由①②可得:xP2+3yP2=(x12+3y12)+(x22+3y22)
∵M、N是椭圆上的点,∴x12+3y12=9,x22+3y22=9,
∴xP2+3yP2=18,即$\frac{{{x}_{P}}^{2}}{18}+\frac{{{y}_{P}}^{2}}{6}$=1.
∴动点P在定曲线$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{6}=1$上.
点评 本题考查双曲线方程的求法,考查三角形面积的求法,考查动点在定曲线上的证明,是中档题,解题时要认真审题,注意椭圆、双曲线性质的合理运用.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
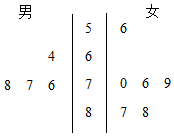 一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点P在△ABC外,且△APC的面积为$\frac{1}{3}$S | B. | 点P在△ABC外,且△APC的面积为$\frac{1}{2}$S | ||
| C. | 点P在△ABC内,且△APC的面积为$\frac{1}{3}$S | D. | 点P在△ABC内,且△APC的面积为$\frac{1}{2}$S |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
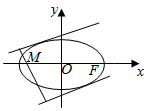 已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.
已知点F(1,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且椭圆C上的点到点F的最大距离为$\sqrt{2}+1$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
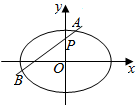 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com