
分析 (1)由于对任意n∈N+都有a31+a32+a33+…+a3n=S2n+2Sn.an>0(n∈N*).分别令n=1,2,解出即可得出.
(2)对任意n∈N+都有a31+a32+a33+…+a3n=S2n+2Sn.an>0(n∈N*).利用递推关系化为:${a}_{n}^{2}$=Sn+Sn-1+2,又${a}_{n+1}^{2}$=Sn+1+Sn+2,再一次利用递推关系可得:${a}_{n+1}^{2}$-${a}_{n}^{2}$=an+1+an,化为an+1-an=1,利用等差数列的通项公式可得:an=n+1.3${\;}^{{a}_{n}}$-26an=3n+1-26(n+1).可知:当n=1,2,3时,3${\;}^{{a}_{n}}$-26an<0.n≥4时,3${\;}^{{a}_{n}}$-26an>0.即可得出数列{3${\;}^{{a}_{n}}$-26an}的前n项和Tn的最小值为T3.
(3)由bn=3n+(-1)n-1•t•2${\;}^{{a}_{n}}$,对任意n∈N+都有bn+1>bn恒成立,可得3n+1+(-1)n•t$•{2}^{{a}_{n+1}}$>3n+(-1)n-1•t•2${\;}^{{a}_{n}}$,化为:2×3n>(-1)n-1•t•2n+1-(-1)n•t•2n+2.对n分类讨论,利用数列的单调性即可得出.
解答 解:(1)∵对任意n∈N+都有a31+a32+a33+…+a3n=S2n+2Sn.an>0(n∈N*).
分别令n=1,2,可得:${a}_{1}^{3}$=${S}_{1}^{2}$+2S1=${a}_{1}^{2}+2{a}_{1}$,a31+a32=${S}_{2}^{2}+2{S}_{2}$=$({a}_{1}+{a}_{2})^{2}$+2(a1+a2).
联立解得a1=2,a2=3.
(2)对任意n∈N+都有a31+a32+a33+…+a3n=S2n+2Sn.an>0(n∈N*).
当n≥2时,a31+a32+a33+…+${a}_{n-1}^{3}$=${S}_{n-1}^{2}$+2Sn-1.
∴${a}_{n}^{3}$=S2n+2Sn-${S}_{n-1}^{2}$-2Sn-1.
化为:${a}_{n}^{2}$=Sn+Sn-1+2,
又${a}_{n+1}^{2}$=Sn+1+Sn+2,
∴${a}_{n+1}^{2}$-${a}_{n}^{2}$=an+1+an,
化为an+1-an=1,又a2-a1=1,
∴数列{an}是等差数列,首项为2,公差为1.
∴an=2+(n-1)=n+1.
∴3${\;}^{{a}_{n}}$-26an=3n+1-26(n+1).
当n=1时,${3}^{{a}_{1}}-26{a}_{1}$=9-26×2<0,
同理可得:n=2,3时,3${\;}^{{a}_{n}}$-26an<0.
n≥4时,3${\;}^{{a}_{n}}$-26an>0.
∴数列{3${\;}^{{a}_{n}}$-26an}的前n项和Tn的最小值为T3=32+33+34-26×(2+3+4)=-117.
(3)∵bn=3n+(-1)n-1•t•2${\;}^{{a}_{n}}$,对任意n∈N+都有bn+1>bn恒成立,
∴3n+1+(-1)n•t$•{2}^{{a}_{n+1}}$>3n+(-1)n-1•t•2${\;}^{{a}_{n}}$,
化为:2×3n>(-1)n-1•t•2n+1-(-1)n•t•2n+2.
当n为偶数时,化为:2×3n>-t•2n+1-t•2n+2,t>$-\frac{1}{3}×(\frac{3}{2})^{n}$的最大值,∴t>$-\frac{1}{3}×(\frac{3}{2})^{2}$=-$\frac{3}{4}$.
当n为奇数时,化为:2×3n>t•2n+1+t•2n+2,化为t<$\frac{1}{3}×(\frac{3}{2})^{n}$的最小值,∴t<$\frac{1}{2}$.
综上可得:实数t的取值范围是$(-\frac{3}{4},\frac{1}{2})$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法、不等式的性质、递推关系、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于难题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}[{1+{{(-1)}^{n+1}}}]$ | B. | ${sin^2}\frac{nπ}{2}$ | C. | $\frac{1}{2}[{1+{{(-1)}^n}}]$ | D. | $\frac{1-cosnπ}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
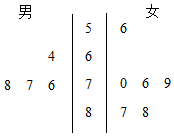 一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com