
 某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.分析 (1)由直方图能求出第四、五组的频率.
(2)由直方图知,第二、三组客户人数分别为10人和20人,所以抽出的6人中,第二组有2人,第三组有4人,由此利用列举法能求出得到奖励的人来自不同组的概率.
解答 解:(1)由直方图知,第四组的频率为0.175×2=0.35,
第五组的频率为0.15×2=0.30,
所以第四、五组的频率分别为0.35和0.3.…(4分)
(2)由直方图知,第二、三组客户人数分别为10人和20人,
所以抽出的6人中,第二组有2人,设为A,B,第三组有4人,设为a,b,c,d.
从中随机抽取2人的所有情况如下:
AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种.…(8分)
其中,两人来自不同组的情况共有8种,…(10分)
所以,得到奖励的人来自不同组的概率为$\frac{8}{15}$. …(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N⊆M | B. | M⊆N | C. | M∩N=∅ | D. | M∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
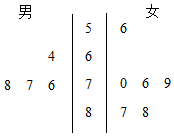 一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.
一所学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| t | 30 | 40 | p | 50 | 70 |
| m | 2 | 4 | 5 | 6 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点P在△ABC外,且△APC的面积为$\frac{1}{3}$S | B. | 点P在△ABC外,且△APC的面积为$\frac{1}{2}$S | ||
| C. | 点P在△ABC内,且△APC的面积为$\frac{1}{3}$S | D. | 点P在△ABC内,且△APC的面积为$\frac{1}{2}$S |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com