Question

5£®º¯Êýf£¨x£©=$\frac{b}{|x|-a}$£¨a£¾0£¬b£¾0£©£¬ÒòÆäͼÏóÀàËÆÓÚºº×Ö¡°‡å¡±×Ö£¬±»³ÆΪ¡°‡åº¯Êý¡±£¬ÎÒÃǰѺ¯Êýf£¨x£©µÄͼÏóÓëyÖáµÄ½»µã¹ØÓÚÔ­µãµÄ¶Ô³Æµã³ÆΪº¯Êýf£¨x£©µÄ¡°‡åµã¡±£¬ÒÔº¯Êýf£¨x£©µÄ¡°‡åµã¡±ÎªÔ²ÐÄ£¬Ó뺯Êýf£¨x£©µÄͼÏóÓй«¹²µãµÄÔ²£¬½Ô³Æº¯Êýf£¨x£©µÄ¡°‡åÔ²¡±£¬Ôòµ±a=b=1ʱ£¬ÓÐÏÂÁÐÃüÌ⣺
¢Ù¶ÔÈÎÒâx¡Ê£¨0£¬+¡Þ£©£¬¶¼ÓÐf£¨x£©£¾$\frac{1}{x}$³ÉÁ¢£»
¢Ú´æÔÚx₀¡Ê£¨$\frac{¦Ð}{6}$£¬$\frac{¦Ð}{3}$£©£¬Ê¹f£¨x₀£©£¼tanx₀³ÉÁ¢£»
¢Ûº¯Êýf£¨x£©µÄ¡°‡åµã¡±Ó뺯Êýy=lnxͼÏóÉϵĵãµÄ×î¶Ì¾àÀëÊÇ$\sqrt{2}$£»
¢Üº¯Êýf£¨x£©µÄËùÓС°‡åÔ²¡±ÖУ¬ÆäÖܳ¤µÄ×îСֵΪ2$\sqrt{3}$¦Ð£®
ÆäÖеÄÕýÈ·ÃüÌâÓТڢۢܣ¨Ð´³öËùÓÐÕýÈ·ÃüÌâµÄÐòºÅ£©£®

Answer 1

·ÖÎö ÀûÓÃÌØÊâÖµ·¨£¬Ñо¿º¯ÊýµÄÖµÓò£¬µ¥µ÷ÐÔ£¬ºÍÁãµãÎÊÌ⣬ÒÔ¼°µ¼ÊýµÄ¼¸ºÎÒâÒ壬ÀûÓÃÊýÐνáºÏµÄ·½·¨½øÐÐÅжϣ®

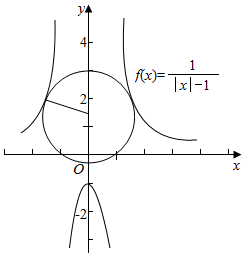½â´ð ½â£ºµ±a=1£¬b=1ʱ£¬º¯Êýf£¨x£©=$\frac{1}{|x|-1}$£¬
¢Ùµ±x=$\frac{1}{2}$ʱ£¬f£¨$\frac{1}{2}$£©=$\frac{1}{\frac{1}{2}-1}$=-2£¬$\frac{1}{\frac{1}{2}}$=2£¬¹Êf£¨x£©£¾$\frac{1}{x}$²»³ÉÁ¢£¬¹Ê¢Ù²»ÕýÈ·£»
¢Úµ±x₀=$\frac{¦Ð}{4}$ʱ£¬f£¨$\frac{¦Ð}{4}$£©=$\frac{1}{\frac{¦Ð}{4}-1}$£¼0£¬tan$\frac{¦Ð}{4}$=1£¬¹Ê´æÔÚx₀¡Ê£¨$\frac{¦Ð}{6}$£¬$\frac{¦Ð}{3}$£©£¬Ê¹f£¨x₀£©£¼tanx₀³ÉÁ¢£¬¹Ê¢ÚÕýÈ·£»
¢ÛÔòº¯Êýf£¨x£©=$\frac{1}{|x|-1}$ÓëyÖá½»ÓÚ£¨0£¬-1£©µã£¬Ôò¡°‡åµã¡±×ø±êΪ£¨0£¬1£©£¬
Éèy=lnx£¬
Ôòy¡ä=$\frac{1}{x}$£¬
ÉèÇеãΪ£¨x₀£¬lnx₀£©£¬
¡àÇÐÏßµÄбÂÊk=$\frac{1}{{x}_{0}}$£¬
µ±¡°‡åµã¡±ÓëÇеãµÄÁ¬Ïß´¹Ö±ÇÐÏßʱ£¬¾àÀë×î¶Ì£¬
¡à$\frac{ln{x}_{0}-1}{{x}_{0}}$•$\frac{1}{{x}_{0}}$=-1£¬
½âµÃx₀=1£¬
¡àÇеã×ø±êΪ£¨1£¬0£©£¬
¹Êº¯Êýf£¨x£©µÄ¡°‡åµã¡±Ó뺯Êýy=lnxͼÏóÉϵĵãµÄ×î¶Ì¾àÀëÊÇ$\sqrt{£¨1-0£©^{2}+£¨0-1£©^{2}}$=$\sqrt{2}$£¬¹Ê¢ÛÕýÈ·£¬
¢ÜÁî¡°‡åÔ²¡±µÄ±ê×¼·½³ÌΪx²+£¨y-1£©²=r²£¬
Áî¡°‡åÔ²¡±Óëf£¨x£©=$\frac{1}{|x|-1}$ͼÏóµÄ×óÓÒÁ½Ö§ÏàÇУ¬
ÔòÇеã×ø±êΪ£¨$\frac{\sqrt{5}+1}{2}$£¬$\frac{\sqrt{5}+1}{2}$£©¡¢£¨-$\frac{\sqrt{5}+1}{2}$£¬$\frac{\sqrt{5}+1}{2}$£©¡¢´Ëʱr=$\sqrt{3}$£»
Áî¡°‡åÔ²¡±Óëf£¨x£©=$\frac{1}{|x|-1}$ͼÏóµÄÏÂÖ§ÏàÇÐ
ÔòÇеã×ø±êΪ£¨0£¬-1£©
´Ëʱr=2£¬
¹Êº¯Êýf£¨x£©µÄËùÓС°‡åÔ²¡±ÖУ¬ÆäÖܳ¤µÄ×îСֵΪ2$\sqrt{3}$¦Ð£¬¹Ê¢ÜÕýÈ·£¬
×ÛÉÏËùÊö£ºÆäÖеÄÕýÈ·ÃüÌâÓТڢۢܣ¬
¹Ê´ð°¸Îª£º¢Ú¢Û¢Ü

µãÆÀ ±¾Ì⿼²éµÄ֪ʶµãÊdzéÏóº¯Êý¼°ÆäÓ¦Óã¬ÆäÖиù¾Ý¡°‡åÔ²¡±µÄÔ²ÐÄ×ø±ê¼°¡°‡åº¯Êý¡±µÄ½âÎöʽ£¬µ¼ÊýµÄ¼¸ºÎÒâÒ壬×î¶Ì¾àÀ룬ÊôÄÑÌ⣮