练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．将5本不同的书分给甲、乙、丙三人，每人至少一本至多两本，则不同的分法种数是（　　）
    A．60B．90C．120D．180

    分析 根据题意，分2步进行分析：①、5本不同的书分成3组，一组1本．剩余两个组每组2本，利用组合数公式可得其分组方法数目，②、将分好的三组全排列，对应甲、乙、丙三人，由排列数公式可得其情况数目，进而由分步计数原理计算可得答案．

    解答 解：根据题意，分2步进行分析：
    ①、5本不同的书分成3组，一组1本．剩余两个组每组2本；
    有$\frac{{C}_{5}^{1}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$=15种分组方法；
    ②、将分好的三组全排列，对应甲、乙、丙三人，有A33=6种情况，
    则有15×6=90种不同的分法；
    故选：B．

    点评 本题考查排列、组合的综合应用，涉及分步计数原理，注意先依据题意分组，进而全排列，对应三人．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．在正项等差数列{an}中a1和a4是方程x2-10x+16=0的两个根，若数列{log2an}的前5项和为S5且S5∈[n，n+1]，n∈Z，则n=11．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．写出分别满足下列条件的双曲线的标准方程．
    （1）曲线上的点P到点F1（4，0）的距离与它到点F2（4，0）的距离的差的绝对值等于6．
    （2）曲线上的点P到点F1（-10，0）的距离与它到点F2（10，0）的距离的差等于16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$2=4，|$\overrightarrow{b}$|=2，（$\overrightarrow{a}$+$\overrightarrow{b}$）（3$\overrightarrow{a}$-$\overrightarrow{b}$）=4，则$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在等差数列{an}中，a5+a10+a15+a20=20，则S24=120．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知椭圆C1：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1，圆C2：x2+y2=t经过椭圆C1的焦点．
    （1）设P为椭圆上任意一点，过点P作圆C2的切线，切点为Q，求△POQ面积的取值范围，其中O为坐标原点；
    （2）过点M（-1，0）的直线l与曲线C1，C2自上而下依次交于点A，B，C，D，若|AB|=|CD|，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

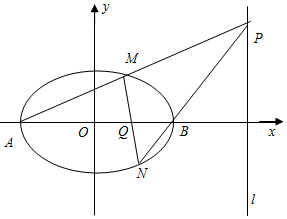    6．在平面直角坐标系xOy中，已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点，离心率为$\frac{1}{2}$，且椭圆过定点$（1，\frac{3}{2}）$，P为椭圆右准线上任意一点，直线PA，PB分别交椭圆于M，N．
    （1）求椭圆的方程；
    （2）若线段MN与x轴交于Q点且$\overrightarrow{MQ}=λ\overrightarrow{QN}$，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设实数a=log32，b=ln2，c=$\frac{1}{{∫}_{0}^{π}sinxdx}$，则（　　）
    A．b＞a＞cB．b＞c＞aC．a＞b＞cD．a＞c＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数g（x）的定义域为{x|x≠0}，且g（x）≠0，设p：函数$f（x）=g（x）（{\frac{1}{{1-{2^x}}}-\frac{1}{2}}）$是偶函数；q：函数g（x）是奇函数，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案