
分析 推导出an=2n,从而log2an=log2(2n)=1+log2n,进而S5=5+log21+log22+log23+log24+log25=8+log215,由此能求出结果.
解答 解:∵在正项等差数列{an}中a1和a4是方程x2-10x+16=0的两个根,
∴a1<a4,解方程得:a1=2,a4=8,d=$\frac{8-2}{4-1}$=2,
∴an=2+(n-1)×2=2n,
∴log2an=log2(2n)=1+log2n,
数列{log2an}的前5项和为S5且S5∈[n,n+1],n∈Z,
∴S5=5+log21+log22+log23+log24+log25=8+log215∈[11,12],
∴n=11.
故答案为:11.
点评 本题考查实数值的求法,考查等差数列性质,考查韦达定理、考查对数性质及运算法则,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

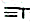 ”表示36,“
”表示36,“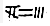 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com