
分析 (Ⅰ)若(x,y)∈A,表示的区域如图所示的正方形,即可求u=x2+y2的取值范围;
(Ⅱ)设集合B={(w,v)|w2+v2=x2+y2,(x,y)∈A},表示的区域是以原点为圆心,$\sqrt{2}$,2为半径的圆环,
即可求集合B表示的区域面积.
解答 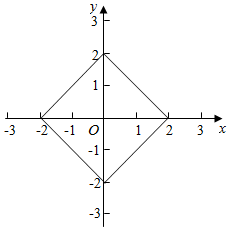 解:(Ⅰ)A={(x,y)||x|+|y|=2}(x,y∈R),表示的区域如图所示的正方形,原点到区域的距离的范围是[$\sqrt{2}$,2],
解:(Ⅰ)A={(x,y)||x|+|y|=2}(x,y∈R),表示的区域如图所示的正方形,原点到区域的距离的范围是[$\sqrt{2}$,2],
∴u=x2+y2的取值范围是[2,4];
(Ⅱ)设集合B={(w,v)|w2+v2=x2+y2,(x,y)∈A},表示的区域是以原点为圆心,$\sqrt{2}$,2为半径的圆环,
∴集合B表示的区域面积是π•22-π•2=2π.
点评 本题考查集合的表示,考查学生的计算能力,正确理解集合是关键.


科目:高中数学 来源: 题型:解答题
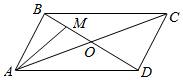 如图,在平行四边形ABCD中,AB=1,AD=2,∠BAD=60°,BD,AC相交于点O,M为BO中点.设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,AB=1,AD=2,∠BAD=60°,BD,AC相交于点O,M为BO中点.设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
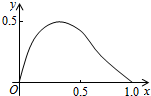 函数f(x)=axm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值可能是②.(填序号)
函数f(x)=axm(1-x)n在区间[0,1]上的图象如图所示,则m,n的值可能是②.(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com