
下列命题中,真命题是
A.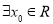 ,使得
,使得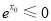
B.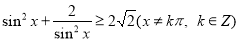
C.
D.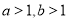 是
是 的充分不必要条件
的充分不必要条件
D
【解析】A.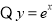 的值域为
的值域为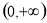 ,所以“
,所以“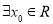 ,使得
,使得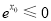 ”是假命题;
”是假命题;
B.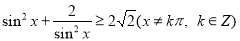 ,当且仅当
,当且仅当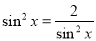 ,即
,即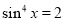 成立(而
成立(而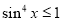 ),
),
所以“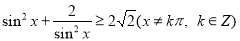 ”为假命题;
”为假命题;
C.当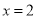 时,
时,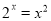 ,所以“
,所以“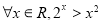 ”为假命题;
”为假命题;
D.当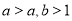 ,由不等式的性质,得
,由不等式的性质,得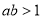 ;而
;而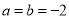 满足
满足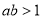 ,不满足
,不满足 ,所以“
,所以“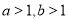 是
是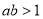 的充分不必要条件”是假命题;故选D.
的充分不必要条件”是假命题;故选D.
考点:命题的判定.
考点分析: 考点1:命题及其关系 考点2:必要条件、充分条件与充要条件的判断 【知识点的认识】正确理解和判断充分条件、必要条件、充要条件和非充分非必要以及原命题、逆命题否命题、逆否命题的概念是本节的重点;掌握逻辑推理能力和语言互译能力,对充要条件概念本质的把握是本节的难点.

科目:高中数学 来源:2014-2015学年甘肃省高三第一次联考文科数学试卷(解析版) 题型:选择题
下列推断错误的是( )
A.命题“若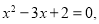 则
则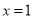 ”的逆否命题为“若
”的逆否命题为“若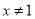 则
则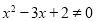 ”
”
B.命题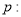 存在
存在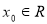 ,使得
,使得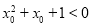 ,则非
,则非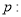 任意
任意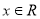 ,都有
,都有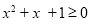
C.若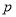 且
且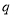 为假命题,则
为假命题,则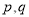 均为假命题
均为假命题
D.“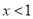 ”是“
”是“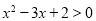 ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查文科数学试卷(解析版) 题型:选择题
现有四个函数:① ;②
;②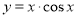 ;③
;③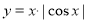 ; ④
; ④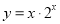 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是
的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是
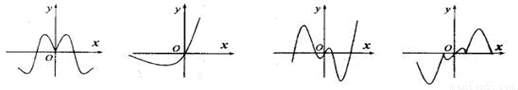
A.④①②③ B.①④③② C.①④②③ D.③④②①
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:填空题
如图所示,记正方体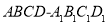 的中心为
的中心为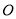 ,面
,面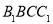 的中心为
的中心为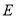 ,
,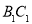 的中点为
的中点为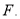 则空间四边形
则空间四边形 在该正方体各个面上的投影可能是 .(把你认为正确命题的序号填写在答题纸上)
在该正方体各个面上的投影可能是 .(把你认为正确命题的序号填写在答题纸上)

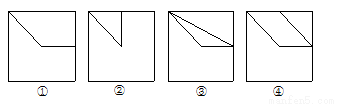
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:选择题
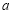 为如图所示的程序框图中输出的结果,则化简
为如图所示的程序框图中输出的结果,则化简 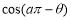 的结果是
的结果是

A.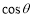 B.
B.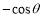 C.
C.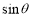 D.
D.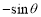
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题13分)已知函数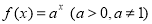 在区间[-1,2]上的最大值是最小值的8倍.
在区间[-1,2]上的最大值是最小值的8倍.
(Ⅰ)求a的值;
(Ⅱ)当a>1时,解不等式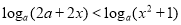 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省高二上学期期末考试文科数学试卷(解析版) 题型:填空题
设直线x-3y+m=0(m≠0)与双曲线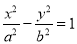 (a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 .
(a>0, b>0)的两条渐近线分别交于A、B两点,若P(m, 0)满足|PA|=|PB|,则该双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省文登市高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知椭圆与双曲线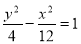 的焦点相同,且它们的离心率之和等于
的焦点相同,且它们的离心率之和等于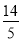 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)过椭圆内一点 作一条弦
作一条弦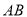 ,使该弦被点
,使该弦被点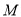 平分,求弦
平分,求弦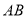 所在直线方程.
所在直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com