
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出f′(1),得到关于a的方程,解出即可求出f(x)的表达式,从而求出函数的单调区间,求出函数的极值,得到符合条件的m的范围即可;
(Ⅲ)问题等价于方程2t3-6t2+3=0有三个不同解,设ϕ(t)=2t3-6t2+3,根据函数的单调性求出ϕ(t)的极大值和极小值,从而证出结论.
解答 (Ⅰ)解:f'(x)=3x2-3a=3(x2-a),…(1 分)
当a<0时,对于x∈R,f'(x)>0恒成立,
所以,当a<0时,f(x)在区间(-∞,+∞)上单调递增; …(2 分)
当a>0时,由f'(x)>0,解得$x<-\sqrt{a}$或$x>\sqrt{a}$,
由f'(x)<0,解得$-\sqrt{a}<x<\sqrt{a}$,
所以,当a>0时,f(x)在区间$(-∞{,_{\;}}-\sqrt{a}]$和区间$[\sqrt{a}{,_{\;}}+∞)$上单调递增,
在区间$[-\sqrt{a}{,_{\;}}\sqrt{a}]$上单调递减.…(4 分)
(Ⅱ)解:因为f(x)在x=-1处取得极值,
所以f'(1)=3×(-1)2-3a=0,故a=1.…(5 分)
则f(x)=x3-3x-1,f'(x)=3x2-3,
由f'(x)=0,解得x=-1或x=1.
由(Ⅰ)中f(x)的单调性,可知f(x)在x=-1处取得极大值f(-1)=1,
在x=1处取得极小值f(1)=-3.…(7 分)
因为函数g(x)=f(x)-m有三个零点,
而在极大值点左侧存在f(-3)=-19<f(1),
在极小值点右侧存在f(3)=17>f(-1),
所以m<f(-1)且m>f(1),即实数m的取值范围(-3,1).…(9 分)
(Ⅲ)证明:依题意,h(x)=(x3-3ax-1)+(3a-1)x+1=x3-x,…(10分)
则h(x)=x3-x在点(t,h(t))处的切线方程为y=(3t2-1)x-2t3.…(11分)
若切线过点P(2,1),则1=2(3t2-1)-2t3,即2t3-6t2+3=0.
过点P(2,1)可以作曲线h(x)的三条切线等价于
方程2t3-6t2+3=0有三个不同解.…(12分)
设ϕ(t)=2t3-6t2+3,则ϕ'(t)=6t2-12t=6t(t-2),
因为ϕ(t)在R上有唯一极大值ϕ(0)=3>0和唯一极小值ϕ(2)=-5<0,
且在极大值点左侧存在ϕ(-1)=-5<0,在极小值点右侧存在ϕ(3)=3>0,
因此方程ϕ(t)=0有三个不同解.
所以过点P(2,1)可以作曲线h(x)的三条切线.…(14分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,考查函数的零点,曲线的切线方程,是一道综合题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
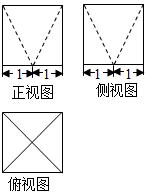
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 工作 效益 机器 | 一 | 二 | 三 | 四 | 五 |
| 甲 | 15 | 17 | 14 | 17 | 15 |
| 乙 | 22 | 23 | 21 | 20 | 20 |
| 丙 | 9 | 13 | 14 | 12 | 10 |
| 丁 | 7 | 9 | 11 | 9 | 11 |
| 戊 | 13 | 15 | 14 | 15 | 11 |
| A. | 甲只能承担第四项工作 | B. | 乙不能承担第二项工作 | ||
| C. | 丙可以不承担第三项工作 | D. | 获得的效益值总和为78 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
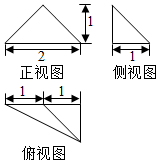
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
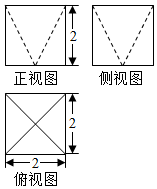
| A. | 4cm3 | B. | 8cm3 | C. | $\frac{16}{3}$cm3 | D. | $\frac{32}{3}$cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com