
【题目】已知函数![]() ,其中a为非零常数.
,其中a为非零常数.
![]() 讨论
讨论![]() 的极值点个数,并说明理由;
的极值点个数,并说明理由;
![]() 若
若![]() ,
,![]() 证明:
证明:![]() 在区间
在区间![]() 内有且仅有1个零点;
内有且仅有1个零点;![]() 设
设![]() 为
为![]() 的极值点,
的极值点,![]() 为
为![]() 的零点且
的零点且![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)(i)证明见解析;(ii)证明见解析.
【解析】
![]() 先对函数求导,然后结合导数与单调性的关系,对a进行分类讨论即可求解函数的单调性,进而可确定极值,
先对函数求导,然后结合导数与单调性的关系,对a进行分类讨论即可求解函数的单调性,进而可确定极值,
![]() 转化为证明
转化为证明![]() 只有一个零点,结合函数与导数知识可证;
只有一个零点,结合函数与导数知识可证;
![]() 由题意可得,
由题意可得,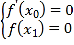 ,代入可得,
,代入可得,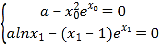 ,结合函数的性质可证.
,结合函数的性质可证.
解:![]() 解:由已知,
解:由已知,![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() ,从而
,从而![]() ,
,
所以![]() 在
在![]() 内单调递减,无极值点;
内单调递减,无极值点;
②当![]() 时,令
时,令![]() ,
,
则由于![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 上有且仅有一个极值点.
上有且仅有一个极值点.
综上所述,当![]() 时,函数
时,函数![]() 无极值点;当
无极值点;当![]() 时,函数
时,函数![]() 只有一个极值点;
只有一个极值点;
![]() 证明:
证明:![]() 由
由![]() 知
知![]() .
.
令![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 内有唯一解,从而
内有唯一解,从而![]() 在
在![]() 内有唯一解,
内有唯一解,
不妨设为![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 是
是![]() 的唯一极值点.
的唯一极值点.
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 内单调递减,
内单调递减,
从而当![]() 时,
时,![]() ,所以
,所以![]() .
.
从而当![]() 时,
时,![]() ,且
,且![]()
又因为![]() ,故
,故![]() 在
在![]() 内有唯一的零点.
内有唯一的零点.
![]() 由题意,
由题意,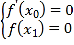 即
即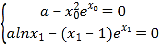 ,
,
从而![]() ,即
,即![]() .
.
因为当![]() 时,
时,![]() ,又
,又![]() ,
,
故![]() ,即
,即![]() ,
,
两边取对数,得![]() ,
,
于是![]() ,整理得
,整理得![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”:①
阶“期待数列”:①![]() ;②
;②![]() .
.
(1)若等比数列![]() 为
为![]() 阶“期待数列”
阶“期待数列”![]() ,求公比
,求公比![]() ;
;
(2)若一个等差数列![]() 既是
既是![]() 阶“期待数列”又是递增数列
阶“期待数列”又是递增数列![]() ,求该数列的通项公式;
,求该数列的通项公式;
(3)记![]() 阶“期待数列”
阶“期待数列” ![]() 的前
的前![]() 项和为
项和为![]() ,求证;数列
,求证;数列![]() 不能为
不能为![]() 阶“期待数列”.
阶“期待数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月18日国际射联步手枪世界杯总决赛在莆田市综合体育馆开幕,这是国际射联步手枪世界杯总决赛时隔10年再度走进中国.为了增强趣味性,并实时播报现场赛况,我校现场小记者李明和播报小记者王华设计了一套播报转码法,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的![]() 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式:
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式: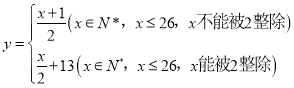 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即
,即![]() 变换成
变换成![]() ,即
,即![]() 变换成
变换成![]() .若按上述规定,若王华收到的密文是
.若按上述规定,若王华收到的密文是![]() ,那么原来的明文是( )
,那么原来的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月26日,甘肃省人民政府办公厅发布《甘肃省关于餐饮业质量安全提升工程的实施意见》,卫生部对16所大学食堂的“进货渠道合格性”和“食品安全”进行量化评估.满10分者为“安全食堂”,评分7分以下的为“待改革食堂”.评分在4分以下考虑为“取缔食堂”,所有大学食堂的评分在7~10分之间,以下表格记录了它们的评分情况:

(1)现从16所大学食堂中随机抽取3个,求至多有1个评分不低于9分的概率;
(2)以这16所大学食堂评分数据估计大学食堂的经营性质,若从全国的大学食堂任选3个,记![]() 表示抽到评分不低于9分的食堂个数,求
表示抽到评分不低于9分的食堂个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
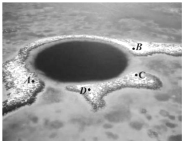
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1000元,则气体费用最少为( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目,A、B两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将A队第六位选手的成绩没有给出,并且告知大家B队的平均分比A队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
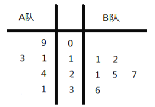
(1)根据茎叶图中的数据,求出A队第六位选手的成绩;
(2)主持人从A队所有选手成绩中随机抽取2个,求至少有一个为“晋级”的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com