
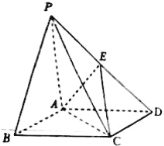
【题目】如图,在四棱锥P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=![]() AC,E是PD的中点,求证:
AC,E是PD的中点,求证:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
【答案】(1)见解析(2)见解析
【解析】
(1)连结BD,交AC于点O,连OE,根据底面图像的特点得到O为BD的中点又E是PD的中点,故OE∥PB,进而得到线面平行;(2)根据底面ABCD是菱形,∠ABC=60°,所以![]() 为正三角形,通过边长关系得到PB =
为正三角形,通过边长关系得到PB =![]() AB =
AB =![]() PA,从而,PA⊥AB,同理可证PA⊥AD进而得到PA⊥平面ABCD,再由面面垂直的判定得到平面PAC⊥平面ABCD.
PA,从而,PA⊥AB,同理可证PA⊥AD进而得到PA⊥平面ABCD,再由面面垂直的判定得到平面PAC⊥平面ABCD.
(1)连结BD,交AC于点O,连OE.
因为底面ABCD是菱形,
所以点O为BD的中点.
又E是PD的中点,故OE∥PB.
又因为OE![]() 平面ACE,PB
平面ACE,PB![]() 平面ACE.
平面ACE.
(2)因为底面ABCD是菱形,∠ABC=60°,
所以![]() 为正三角形,从而AB = AC.
为正三角形,从而AB = AC.
又PB =![]() AC,PA = AC,
AC,PA = AC,
所以PB =![]() AB =
AB =![]() PA.
PA.
从而,PA⊥AB.
同理可证PA⊥AD,
又因为AB![]() AD = A,且AB,AD
AD = A,且AB,AD![]() 平面ABCD,
平面ABCD,
所以PA⊥平面ABCD.
因为PA![]() 平面PAC,所平面PAC⊥平面ABCD.
平面PAC,所平面PAC⊥平面ABCD.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某公司有男性职工64名,一次体检后,将他们的体重(单位:kg)分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为
,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为![]() .
.

(1)求这64名男职工中,体重小于60kg的人数;
(2)从体重在![]() kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件
kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,直角梯形
,直角梯形![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起来,使平面
折起来,使平面![]() 平面
平面![]() .如图
.如图![]() ,设
,设![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 的中点为
的中点为![]() .
.
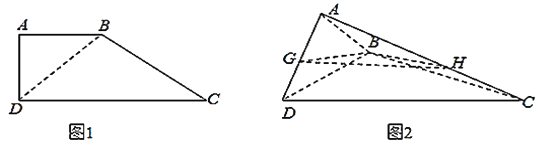
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )求平面
)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(![]() )在线段
)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在确定点
,若存在确定点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=![]() AC,AE=
AC,AE=![]() AB,BD,CE相交于点F.
AB,BD,CE相交于点F.
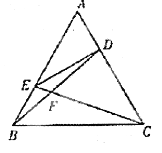
(Ⅰ)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
收看人数 | 14 | 30 | 16 | 28 | 20 | 12 |
(1)若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:
男 | 女 | 合计 | |
体育达人 | 40 | ||
非体育达人 | 30 | ||
合计 |
并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.求抽取的这两人恰好是一男一女的概率.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
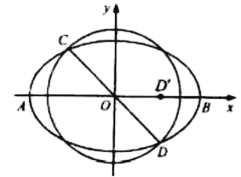
【题目】如图,已知AB为椭圆E:![]() (a>b>0)的长轴,过坐标原点O且倾斜角为135°的直线交椭圆E于C,D两点,且D在x轴上的射影D'恰为椭圆E的长半轴OB的中点.
(a>b>0)的长轴,过坐标原点O且倾斜角为135°的直线交椭圆E于C,D两点,且D在x轴上的射影D'恰为椭圆E的长半轴OB的中点.
(1)求椭圆E的离心率;
(2)若AB=8,不过第四象限的直线l与椭圆E和以CD为直径的圆均相切,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考公式:回归直线![]() ,其中
,其中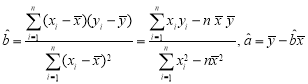 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com