
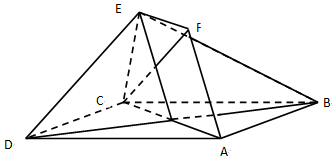
 (文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.
(文)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,EF=CE,AB=$\sqrt{2}$EF.分析 (Ⅰ)设AC于BD交于点G.证明AF∥EG,然后证明AF∥平面BDE.
(Ⅱ)连接FG.证明CF⊥EG,BD⊥AC.CF⊥BD.然后证明CF⊥平面BDE.
解答 证明:(Ⅰ)设AC于BD交于点G.因为EF∥AG,且EF=1,AG=$\frac{1}{2}$AG,
所以四边形AGEF为平行四边形
所以AF∥EG
因为EG?平面BDE,AF?平面BDE,
所以AF∥平面BDE
(Ⅱ)连接FG.因为EF∥CG,EF=CG=CE,所以平行四边形CEFG为菱形.
所以CF⊥EG.
因为四边形ABCD为正方形,所以BD⊥AC.
又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
所以BD⊥平面ACEF.
所以CF⊥BD.又BD∩EG=G,
所以CF⊥平面BDE.
点评 本题考查直线与平面垂直以及直线与平面平行的判定定理以及性质定理的应用,考查空间想象能力以及逻辑推理能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com