练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知△ABC中，AB=$\sqrt{3}$，AC=1，∠CAB=30°，则△ABC的面积为（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{1}{2}$C．$\sqrt{3}$D．$\frac{\sqrt{3}}{4}$

    分析 根据题意和三角形的面积公式直接求出△ABC的面积．

    解答 解：∵△ABC中，AB=$\sqrt{3}$，AC=1，∠CAB=30°，
    ∴△ABC的面积S=$\frac{1}{2}•AB•AC•sin∠CAB$
    =$\frac{1}{2}×\sqrt{3}×1×sin30°$=$\frac{1}{2}×\sqrt{3}×\frac{1}{2}$=$\frac{\sqrt{3}}{4}$，
    故选：D．

    点评 本题考查了三角形的面积公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．已知集合A={x|1≤x≤7}，B={x|1-2m＜x＜m+2}，U=R．若A∩B=B，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

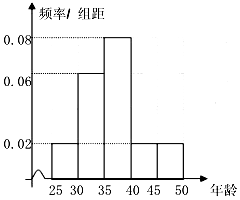    18．我校名教师参加我县“六城”同创“干部职工进网络，服务群众进社区”活动，他们的年龄均在25岁至50岁之间，按年龄分组：第一组[25，30），第二组[30，35），第三组[35，40），第四组[40，45），第五组[45，50]，得到的频率分布直方图如图所示：
    区间[25，30）[30，35）[35，40）[40，45）[45，50]
    人数5ab
    如表是年龄的频数分布表．
    （1）求正整数a，b，N的值；
    （2）根据频率分布直方图估计我校这N名教师年龄的中位数和平均数；
    （3）从第一、二组用分层抽样的方法抽取4人，现在从这4人中任取两人接受咸丰电视台的采访，求从这4人中选取的两人年龄均在第二组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F2，左准线是l，若该双曲线右支上存在点P，使PF2等于P到直线l的距离，则该双曲线离心率的取值范围是（1，$\sqrt{2}+1]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=log2$\frac{1+x}{1-x}$．
    （Ⅰ）判断f（x）奇偶性并证明；
    （Ⅱ）用单调性定义证明函数g（x）=$\frac{1+x}{1-x}$在函数f（x）定义域内单调递增，并判断f（x）=log2$\frac{1+x}{1-x}$在定义域内的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=2x2-kx-4在区间[-2，4]上具有单调性，则k的取值范围是（　　）
    A．[-8，16]B．（-∞，-8]∪[16，+∞）C．（-∞，-8）∪（16，+∞）D．[16，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知奇函数$f（x）=\left\{{\begin{array}{l}{-{x^2}+2x}\\ 0\\{{x^2}+2x}\end{array}\begin{array}{l}{（{x＞0}）}\\{（{x=0}）}\\{（{x＜0}）}\end{array}}\right.$
    （1）在直角坐标系中画出y=f（x）的图象，并指出函数的单调区间；
    （2）若函数f（x）在区间[-1，a-2]上单调递增，试确定a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）的定义域为（0，4），函数g（x）=f（x+1）的定义域为集合A，集合B={x|a＜x＜2a-1}，若A∩B=B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

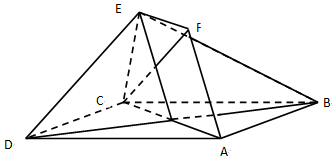    17．（文）如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，EF=CE，AB=$\sqrt{2}$EF．
    （Ⅰ）求证：AF∥平面BDE；
    （Ⅱ）求证：CF⊥平面BDE．

    查看答案和解析>>

    同步练习册答案