
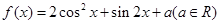 .
.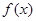 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;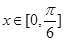 时,
时,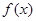 的最大值为2,求
的最大值为2,求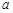 的值,并求出
的值,并求出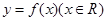 的对称轴方程.
的对称轴方程. 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源:不详 题型:单选题
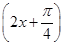 和函数y=cos
和函数y=cos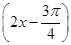 的图象关于原点对称;命题q:当x=kπ+
的图象关于原点对称;命题q:当x=kπ+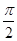 (k∈Z)时,函数y=
(k∈Z)时,函数y=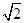 (sin 2x+cos 2x)取得极小值.下列说法正确的是( )
(sin 2x+cos 2x)取得极小值.下列说法正确的是( )| A.p∨q是假命题 | B.¬p∧q是假命题 |
| C.p∧q是真命题 | D.¬p∨q是真命题 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
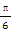 ),那么单摆来回摆动一次所需的时间为( )
),那么单摆来回摆动一次所需的时间为( )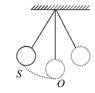
| A.2πs | B.πs | C.0.5s | D.1s |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 与函数g(x)=cos
与函数g(x)=cos ,下列说法正确的是( )
,下列说法正确的是( )| A.函数f(x)和g(x)的图像有一个交点在y轴上 |
| B.函数f(x)和g(x)的图像在区间(0,π)内有3个交点 |
C.函数f(x)和g(x)的图像关于直线x= 对称 对称 |
| D.函数f(x)和g(x)的图像关于原点(0,0)对称 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则(
(-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则( +
+ )·
)· =( )
=( )| A.-32 | B.-16 |
| C.16 | D.32 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
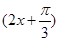 ,则下列结论正确的是( ).
,则下列结论正确的是( ).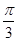 对称;②f(x)的图象关于点
对称;②f(x)的图象关于点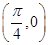 对称;③f(x)的图象向左平移
对称;③f(x)的图象向左平移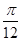 个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在
个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在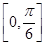 上为增函数
上为增函数| A.①③ | B.②④ | C.①③④ | D.③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com